Teckentabell
Hej
När man ska skissa en graf och jag har en funktion: när jag kommer till steget för tecekntabell så undrar jag. Kan jag använda f(x) För att se om det är växande eller avtagande? För min derivata är ganska krånglig
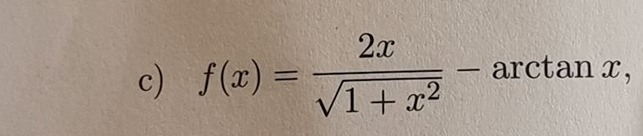

Jag får inte heller rätt värden. Det ska vara 0 på f'(0) men jag får inte det
Ja men då måste du beräkna en otrolig massa punkter. Och då vet du inte ens när du stöter på en extrempunkt, blir nog lite tufft…
Mrpotatohead skrev:Ja men då måste du beräkna en otrolig massa punkter. Och då vet du inte ens när du stöter på en extrempunkt, blir nog lite tufft…
Ohh men på min f'(0) så ska svaret vara 0, men jag får inte 0?
Det är inte så krångligt att derivera den här funktionen. Derivatan till bör du kunna sedan tidigare (men du kan härleda det ganska enkelt också, kan du klura ut hur? :)), och derivatan till den första delen bör du kunna lösa med produktregeln och sedan kedjeregeln.
naytte skrev:Det är inte så krångligt att derivera den här funktionen. Derivatan till bör du kunna sedan tidigare (men du kan härleda det ganska enkelt också, kan du klura ut hur? :)), och derivatan till den första delen bör du kunna lösa med produktregeln och sedan kedjeregeln.
Yes, jag fick fram derivatan också. Men när jag sätter den f'(0) så får jag inte 0 med derivatan. Är min derivata fel då?
Nej, det innebär bara att funktionen inte har en extrempunkt där x=0.
Mrpotatohead skrev:Nej, det innebär bara att funktionen inte har en extrempunkt där x=0.
Nej inte extrempunkten i sig. Utan jag kollar om funktionen är växande eller avtagande innan och efter punkterna. Därför har jag valt ett värde emellan. I facit så korsar funktionen origo
Fast jag lyckas inte få 0 när jag sätter in den

Smaragdalena skrev:
Varför är det så?
f(x) och f'(x) är olika funktioner.
Bara för att f(0) = 0 så behöver det inte gälla att f'(0) = 0.
========
Ett annat exempel på en sådan funktion är f(x) = 2x.
Där gäller att f'(x) = 2 och vi får då att
- f(0) = 2*0 = 0
- f'(0) = 2
Yngve skrev:f(x) och f'(x) är olika funktioner.
Bara för att f(0) = 0 så behöver det inte gälla att f'(0) = 0.
========
Ett annat exempel på en sådan funktion är f(x) = 2x.
Där gäller att f'(x) = 2 och vi får då att
- f(0) = 2*0 = 0
- f'(0) = 2
Wow okej tack🥹🥹





