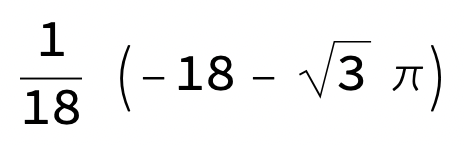Taylorseries
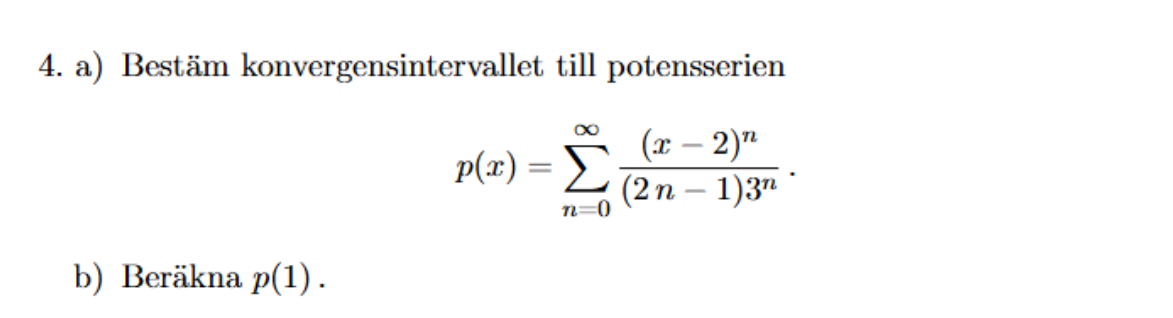 Löste 4a men fastande på 4b, hur ska man tänka?
Löste 4a men fastande på 4b, hur ska man tänka?
Sätt in x=1. Detta ger dig en enkel geometrisk serie som du kan bestämma med hjälp av den slutna formeln för geometrisk serie.
vad är den slutna formeln för geometrisk serie?
vad kommer a och r vara i detta fall? kommer a vara -1^n ?
a är en konstant (som i ditt fall blir 1). r är basen till potensen som ingår i varje term av summan.
Skriv om din summa för x=1 så blir det enklare att identifiera faktorer.
12n-1×(13)n, såhär typ?
-1/3?
Trinity2 skrev:-1/3?
varför blir det negativt?
(1-2)^n = (-1)^n
Svaret
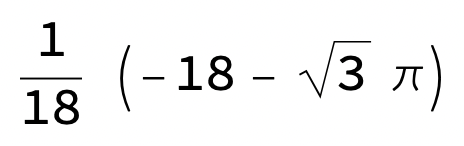
indikerar att detta ej är en geometrisk summa. Är det ett kapitel med Percivals formel eller liknande? Jag minns lite av alla de trick som finns med summor och jag tror vi behöver mera info om vad kapitlet handlar om, ev. något löst exempel i boken. π brukar ramla ut på arctan(1)=π/4 så något sådant är säkert inblandat.
juste, då kan man väll dela upp den (-1)n2n+1×(13)n?
Trinity2 skrev:Svaret
indikerar att detta ej är en geometrisk summa. Är det ett kapitel med Percivals formel eller liknande? Jag minns lite av alla de trick som finns med summor och jag tror vi behöver mera info om vad kapitlet handlar om, ev. något löst exempel i boken. π brukar ramla ut på arctan(1)=π/4 så något sådant är säkert inblandat.
Vi har inte gått igenom percivals formel, utan man ska använda taylor serie
Är du säkert på att boken(?) skrivit rätt. Kör jag detta i ett program får jag
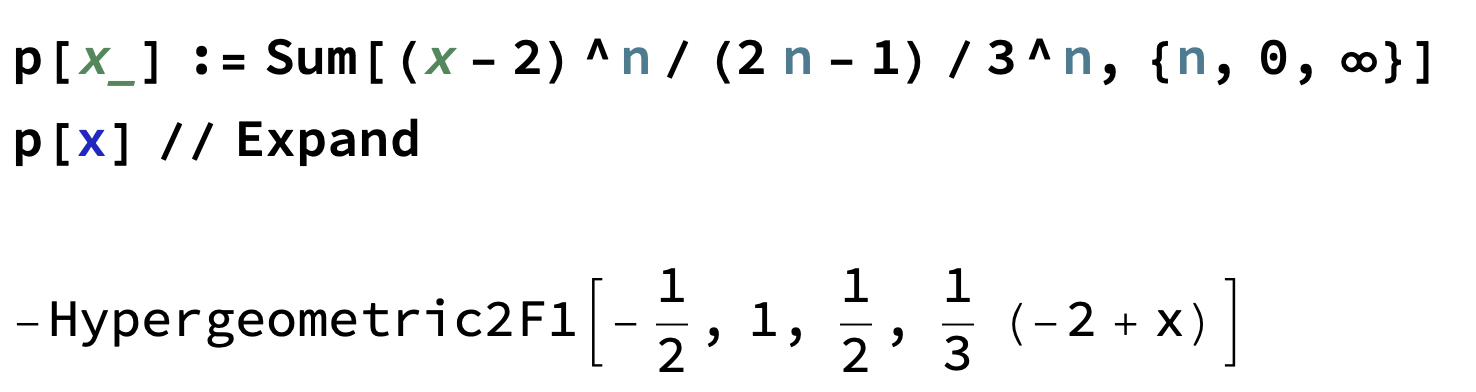
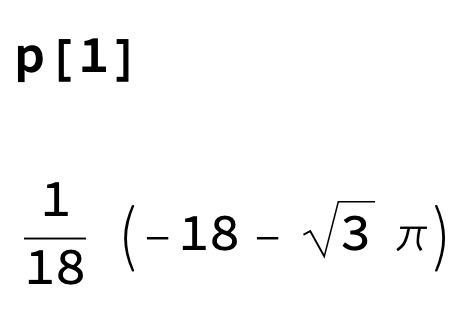
Det är långt ifrån "vanliga" funktioner. Kanske de avser någon speciell metod vid beräkning av p(1)?
svaret i till frågan enligt facit är -1-3
Ah, mitt fel. Misstog n för ett x i nämnaren. Så den formel jag skickade kommer inte fungera.