taylorapproximation av termer
Hej hej!
Har en uppgift här som jag ska approximera mha taylorpolynom. Har dock svårt att avgöra hur jag ska gå tillväga. Funktionen är två termer, ena en trigonometrisk term och den andra under ett rottecken. Ska jag dela upp och derivera dem var för sig och sedan multiplicera ihop resultaten, eller ska jag derivera allt direkt? Inget känns som en bra lösning då derivatan blir lång och krånglig men resultatet av uppdelningen blev också krånglig i slutändan. Finns det någon klok som kan bidra?
Bild på uppg?
Har flera liknande uppgifter. En av dem är . Det finns olika sorters liknande kombinationer med trigonometri, rottecken, naturliga logaritmen och e. Därför jag undrar om det är en möjlig väg att gå att taylorutveckla termerna var för sig för att underlätta deriveringen och sedan sätta ihop dem med multiplikation? Å andra sidan är jag osäker då vi trots allt har produktregler och dyl. just för att det finns särskilda tillvägagångssätt? Men undrar egentligen om man kan genomföra själva taylorutvecklingen av termerna separat och sedan multiplicera resultatet? Det kan tilläggas att några av dem är en utveckling kring punkten 0, vilket också innebär en maclaurinutveckling. Men vet inte om det påverkar svaret.
kaffemedmjolk skrev:Har flera liknande uppgifter. En av dem är . Det finns olika sorters liknande kombinationer med trigonometri, rottecken, naturliga logaritmen och e. Därför jag undrar om det är en möjlig väg att gå att taylorutveckla termerna var för sig för att underlätta deriveringen och sedan sätta ihop dem med multiplikation? Å andra sidan är jag osäker då vi trots allt har produktregler och dyl. just för att det finns särskilda tillvägagångssätt? Men undrar egentligen om man kan genomföra själva taylorutvecklingen av termerna separat och sedan multiplicera resultatet? Det kan tilläggas att några av dem är en utveckling kring punkten 0, vilket också innebär en maclaurinutveckling. Men vet inte om det påverkar svaret.
Vanligtvis skall man använda de standardserieutvecklingar som finns. Ibland krävs att man deriverar, men det är mera sällan.
Hm, men vad är det för den sista termen då? Jag har tolkat det som att man alltid ska derivera?
kaffemedmjolk skrev:Hm, men vad är det för den sista termen då? Jag har tolkat det som att man alltid ska derivera?
Menar du sqrt(x+2)
Om f(x) skall approximeras runt x=a får denna deriveras.
Så här blir serien runt x=a upp till 5:e ordningen
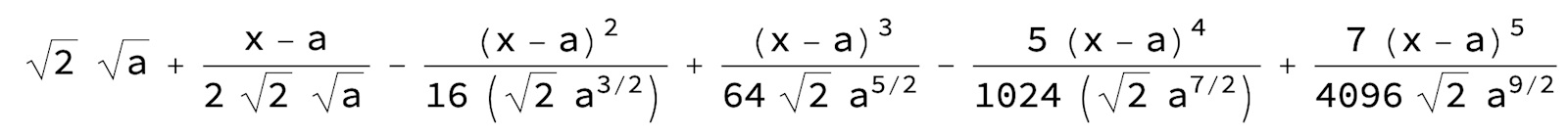
och för x=0
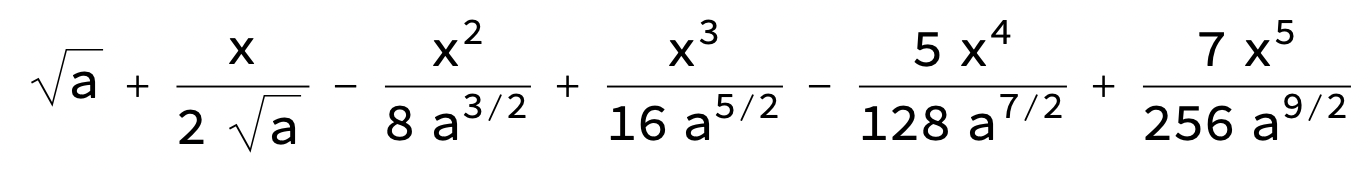
okej så med andra ord är det möjligt att tillfälligt taylorutveckla de olika termerna för sig tills man ska sätta in det i formeln dvs?
kaffemedmjolk skrev:okej så med andra ord är det möjligt att tillfälligt taylorutveckla de olika termerna för sig tills man ska sätta in det i formeln dvs?
Ja, deriverar inte komplicerade produkter eller liknande. Tag varje "basfunktion" för sig och multiplicera sedan polynomen.
Tänk på att t.ex. cos(x^2) så använder du cos(x), men "stoppar in" x^2 på x:s ställe i polynomet.

