Taylor Serie, Närmevärde till en integral.
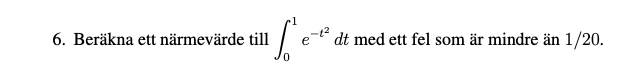
Jag vet inte riktigt hur jag ska tänka kring denna uppgift. Jag vet att man ska använda Taylor serie men inte hur exakt. Jag har deriverat funktionen 3 gånger men vet inte riktigt vad "a" värden blir i Taylor polynomet.
Jag uppfattar a-värdet som den punkt du utvecklar taylorserien kring.
Kom ihåg att taylorserien kommer vara exakt i punkten a, bra approximation i en närliggande omgivning till a och allt sämre approximation ju längre ifrån a vi rör oss.
Därmed vill du välja ett a som är nära det område funktionen ska approximeras i (tänk på att integralen går från 0 till 1).
Jag känner mig fortfarande osäker på uppgiften, jag vet inte ens om hur jag går vidare med taylor formel, jag vet inte hur man ska tänka när man stöter på sådana uppgifter, a värdet kan antigen vara 0 eller 1 men det känns inte rätt heller. 
Sätt att f(t)=e^(-t2). Det är denna funktion du vill approximera mha av ett taylorpolynom.
Värden på a inom intervallet [0,1] är rimliga val. Det bästa vore kanske att sätta a=1/2 (skulle ge snabbast konvergens mot det exakta svaret). Men för enkelhetens skull bör du sätta a=0.
Börja med den vanliga eu. Ta dess Taylor-utveckling runt 0 och sätt u = -t2. Integrera. Sätt in t = 1.
Med Lagranges restterm kan du få kontroll på felet som du enligt uppgiften behöver ha.



