Taylor serie för e^(x^2+y^2)

En känd Maclaurinutveckling för exponentialfunktionen är

$\displaystyle e^{r^2}=\sum_{n=0}^{\infty}\frac{r^{2n}}{n!}$

Kanske är det något man kan använda genom någon sorts substitution eller koordinattransformation?

D4NIEL skrev:

En känd Maclaurinutveckling för exponentialfunktionen är

$\displaystyle e^{r^2}=\sum_{n=0}^{\infty}\frac{r^{2n}}{n!}$

Kanske är det något man kan använda genom någon sorts substitution eller koordinattransformation?

Med den informationen testade jag att skriva $f \left( x,y \right)=\sum_{n=0} ^{ \infty} \dfrac{ \left( x^2+y^2 \right)^n}{n!}$ det verkar dock utveckla i facit. Vet du varför de utvecklar? räcker det inte att skriva som jag gjort och sluta där? 

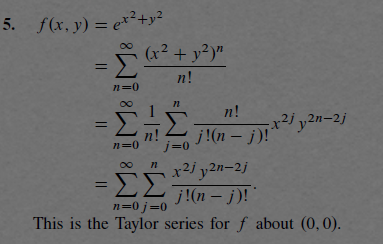
Cien skrev:

det inte att skriva som jag gjort och sluta där? 

Jag tycker det räcker, att binomialutveckla termerna kan man låta en dator eller en doktorand sköta. Det viktiga är att man förstår hur man löser det, inte att man slösar tid på meningslöst harvande.

Med det sagt kan det finnas en poäng i lite sifferexercis, speciellt i början av studierna.