Tangentens ekvation
"Bestäm ekvationen för dom tangenter son från punkten (0;-2) kan dras till kurvan y=0,5x^2"
Eftersom tangentens k-värde=y' bör k=x
och eftersom tangentens värde är -2 när x=0 bör m=-2
då får jag att tangenten T är: T(x)=x^2-2
Men det är fel - varför?
(Tangenten är en rät linje, så inget x2 ska vara med.)
Ta en punkt på kurvan (a,y(a)). Dra en rät linje till (0,-2). Vilken lutning har den? Den ska vara samma som y'(a).
I så fall är lutningen a... men hur använder jag det sen?
Den ska vara lika stor som lutningen från (a,0.5a2) till (0,2).
Hmm, jag tror att jag förstår. Men varför fungerar inte sättet med att direkt ta derivatans värde som k-värde? Förstår att det blir en andragradare, men jag kan inte komma på en teoretisk förklaring till varför det inte fungerar?
Du får två uttryck för k-värdet
1. Derivatan i tangeringspunkten, y'(a) = a.
2. Sekantens lutning mellan tangeringspunkten (a,0.5a2) och (0,-2).
Om dessa lutningar är lika så kommer sekanten uträknad ovan att tangera kurvan då x = a. Du får en ekvation som ger dig möjliga värden på a.
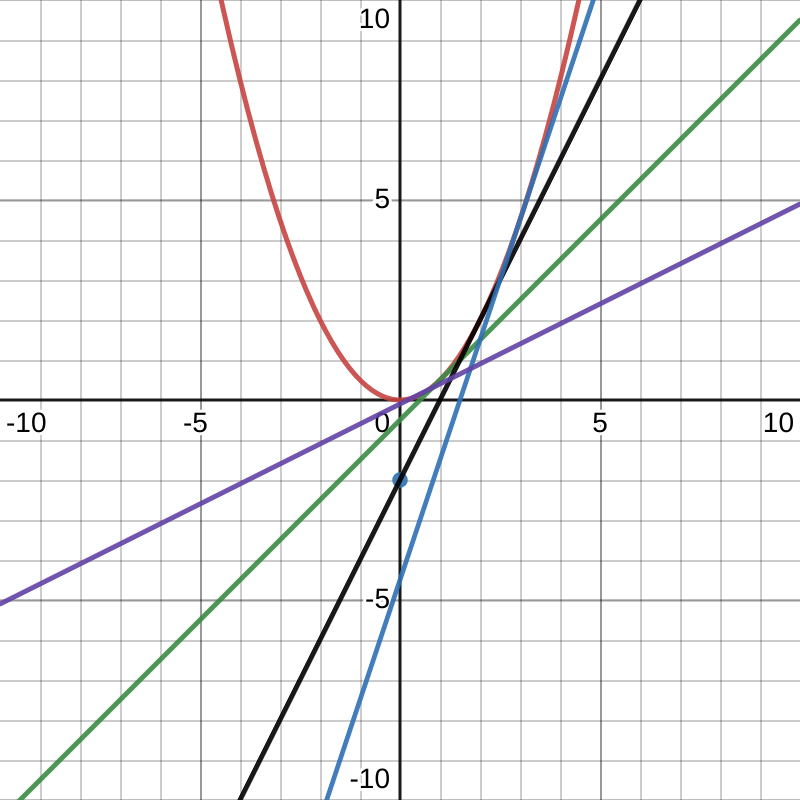
Det är bara en av de här tangenterna som går genom rätt punkt?
Jo, jag förstår att jag med hjälp av k=delta y/delta x till slut får fram att a=±2, men varför kan jag inte direkt sätta k=y'?
Ja, det kan du väl göra, men du vet inte från början för vilket x-värde som tangenten passerar (0,-2).
Dr. G skrev:men du vet inte från början för vilket x-värde som tangenten passerar (0,-2).
Nu klickade det, äntligen!
Det är väl för att bara vissa x-värden har lutningen x som också skär rätt punkt som man måste ställa upp en ekvation för att få fram k?
Sedan tas väl m fram genom det vanliga sättet: att sätta x=0 och sedan y=-2 (=>m=-2)?
Ja, tangenten ska ju gå genom (0, -2).




