Tangent sinx

Hej.

För att en linje ska vara en tangent till en kurva så måste det dels gälla att den har en punkt gemensam med kurvan och att kurvan lutning vid denna punkt är samma som linjens lutning.

Ditt förslag y = cos(pi/3)*x  (dvs y = 0,5x) ör en rät linje som iofs har origo gemensam med sinuskurvan, men sinuskurvan har inte lutningen 0,5 där. Alltså är inte y= 0,5x en tangent till y = sin(x).

Dina övriga uträkningar förstår jag inte. Om du vill ha hjälp med dem så behöver du förklara mer ingående och visa hur du har gjort/tänkt.

=========

Jag föreslår att du

1. Tar fram två x-värden vid vilka sinuskurvan har lutningen 0,5. Detta genom att lösa ekvationen cos(x) = 0,5 
2. Tar fram sinusvärdena för dessa x-värden. Detta ger dig två tangeringspunkter.
3. Tar fram räta linjens ekvationer för tangenterna som har dessa två tangeringspunkter.
4. Visar alla steg i dina uträkningar.

Såhär tänker jag med tangent 1 här, skrev inte ut tangent 2 ifall jag har helt fel.

5π/3 är naturligtvis felsatt i och med att den är från x=0 egentligen 

För att ta reda på m värdet så räknade jag bara med befintligt x värde som ges av enhetscirkeln där cos(x) = 0.5, det vill säga derivatan av sinx.

Fast 0.5 är för ett steg i X, jag går ett halvt till x0 så skillnaden borde bli 0.25. Eller dvs m = -√3

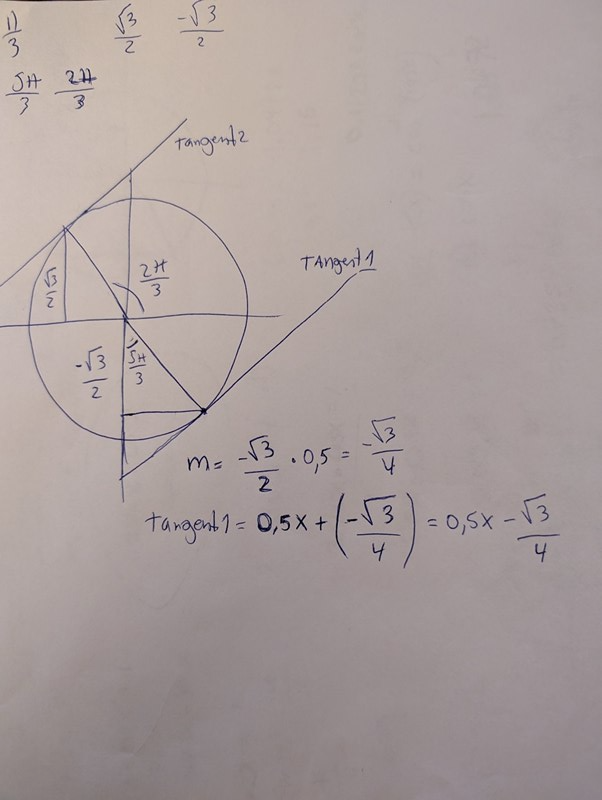
Aha, då förstår jag.

Du har ritat enhetscirkeln, inte en sinuskurva.

Sambandet mellan enhetscirkeln och en sonuskurva är att sinuskurvans horisontella koordinat är lika med vinkeln i enhetscirkeln och sinuskurvans vertikala koordinat är lika med den vertikala koordinaten på enhetscirkeln.

En sinuskurva ser därför ut så här:

Okej men.. ska jag använda en sådan istället alltså tycker du? Eller ja iofs, jag fattar. Dom anger ju funktionen sin och inget annat.

Men hur ska man utefter funktionen där kunna tänka ut några skärningspunkter för y axeln osv.. fattar inte riktigt. Eller det kan man ju genom samma resonemang som i mitt inlägg ovan kanske iofs då.

Dkcre skrev:

[...]

Men hur ska man utefter funktionen där kunna tänka ut några skärningspunkter för y axeln osv.. fattar inte riktigt. Eller det kan man ju genom samma resonemang som i mitt inlägg ovan kanske iofs då.

Följ steg 1-4 i svar #2.

Det är samma metod som du (antagligen) använt tidigare för att hitta tangenters ekvationer.

Här har jag ritat in en av dessa tangenter (det finns oändligt många sådana).

Ja okej.. jag missuppfattade för mycket för att lösa det här. Vill fortfarande tillbaka till enhetscirkeln för att se vart vi skär y axeln av någon anledning men det blir ju helt fel.

När kan en sån här linje vara intressant tro?

Löser den andra imorgon.

Dkcre skrev:

[...]

När kan en sån här linje vara intressant tro?

[...]

Det skulle kunna vara något i stil med "Bestäm ekvationen för de tangenter till enhetscirkeln som har lutningen $\frac{1}{\sqrt{3}}$".

Okej, men ett m värde brukar bara vara ett värde där vi skär y axeln, här anger vi.. 2 stycken värden där vi tangerar sinuskurvan istället? M är inte intressant?

Dkcre skrev:

Okej, men ett m värde brukar bara vara ett värde där vi skär y axeln,

Ja, om vi pratar om räta linjens ekvation y = kx+m så stämmerndet att m är det y-värde där linjen skär y-axeln.

här anger vi.. 2 stycken värden där vi tangerar sinuskurvan istället? M är inte intressant?

Jo, m är intressant om det gäller att bestämma linjens ekvation enligt ovan.

Men om vi bara känner till tangentens lutning k så behöver vi veta koordinaterna för en punkt på linjen för att kunna bestämma k-värdet. Ofta är det enklast att ta fram koordinaterna för just tangeringspunkten.

Men vi pratar alltså inte om räta linjens ekvation här då. Vad är det för sorts ekvation vi pratar om. Så vi anger sinusvärdet och radianvärdet i ekvationen för linjen till det sinusvärdet? Läser man det här rakt av och subtraherar π/6 ifrån √3/2 så blir ju det här helt fel, eller.

Dkcre skrev:

Men vi pratar alltså inte om räta linjens ekvation här då.

Jo, det är räta linjens ekvation som efterfrågas.

Vad är det för sorts ekvation vi pratar om. Så vi anger sinusvärdet och radianvärdet i ekvationen för linjen till det sinusvärdet? Läser man det här rakt av och subtraherar π/6 ifrån √3/2 så blir ju det här helt fel, eller.

Menar du bilden i svar #6? På vilket sätt är den fel menar du?

=====

För att illustrera standardmetoden jag beskrev punktvis i svar #2 så tar vi ett enklare exempel som inte involverar trigonometriska funktioner:

Exempeluppgift: "Bestäm ekvationen för den tangent till parabeln $f(x)=x^2$ som har lutningen 4".

Lösningsförslag steg för steg.

Steg 1: Ta fram de x-värden vid vilka parabeln har lutningen 4. Detta genom att lösa ekvationen $f'(x) = 4$:

Börja med att derivera funktionen: $f'(x)=2x$.

Lös sedan ekvationen $f'(x)=4$, dvs $2x=4$, vilket ger oss den enda lösningen $x=2$.

Steg 2: Ta fram koordinaterna för tangeringspunkten.

Tangeringspunktens x-koordinat är 2. Eftersom tangeringspunkten ligger på parabeln så är dess y-koordinat $f(2)=2^2=4$.

Steg 3: Ta reda på ekvationen för den räta linje som har lutningen 4 och går genom punkten (2, 4).

Vi vet att räta linjens ekvation är $y = kx+m$.

Vi vet att $k = 4$ och att punkten $(x,y)=(2,4)$ uppfyller detta samband, vilket insatt i $y=kx+m$ ger oss ekvationen $4=4\cdot2+m$, dvs $m=-4$.

Svar: Tangentens ekvation är $y=4x-4$

====

Hängde du med på exemplet?

Det är alltså en standardmetod som du kan använda även om det i ditt fall gäller en trigonometrisk funktion istället för en potensfunktion.

======

Försök gärna att tillämpa den här metoden på din uppgift och visa alla räknesteg. Då blir det enklare för oss att förstå var du tappar spåret 

Såhär gjorde jag nu.

Jag tror jag hängde med, hoppas det. Kändes så, i varje fall. Man kan ju dock inte lita helt på sitt eget omdöme.

Verkar ha rätt enligt facit, även om jag föredrog paranteserna där som inte är med i facit. 

Ja, nu ser det bra ut.

Jag saknar bara periodiciteten vid lösningen av ekvationen cos(x) = 0,5.

Hej Yngve,

Tack.

Okej. 

π/3 + n2π

5π/3 + n2π

(?)

Och kanske (0+-π/3) + n2π? Fast det kanske inte riktigt är giltigt att uttrycka sig så.

Det är helt OK att skriva $x=\pm\frac{\pi}{3}+n\cdot2\pi$

Okej tack så mycket. God fortsättning 

Tack detsamma.