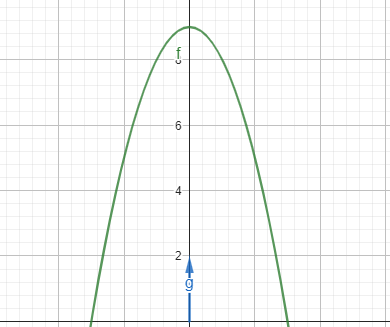
tangent genom 0,2
Har kurvan y = 9-x2 någon tangent som går genom punkten (0,2)
kan någon hjälpa mig på traven?
Börja med att rita en skiss.
- Rita grafen till y = 9-x2.
- Markera punkten (0, 2).
Ser du då vad svaret måste vara?
Om inte så kan du fortsätta med en algebraisk lösning, som innefattar att derivera y = 9-x2 och att se om det går att konstruera någon linje som dels går genom den givna punkten, dels nuddar kurvans graf samtidigt som dess lutning är lila med funktionens derivata i tangeringspunkten.
Yngve skrev:Börja med att rita en skiss.
- Rita grafen till y = 9-x2.
- Markera punkten (0, 2).
Ser du då vad svaret måste vara?
Om inte så kan du fortsätta med en algebraisk lösning, som innefattar att derivera y = 9-x2 och att se om det går att konstruera någon linje som dels går genom den givna punkten, dels nuddar kurvans graf samtidigt som dess lutning är lila med funktionens derivata i tangeringspunkten.
derivatan är -2x
vet inte riktigt hur jag ska konstruera linjen?
räcker det inte bara med att sätta in x och se om det blir samma y-värde där den skär? (alltså 2)
i detta fallet blir det
vilket innebär att svaret blir nej
(kanske helt fel resonemang)
svaret är nej, men jag tror inte att du har full koll på varför.
En tangent är en rät linje, alltså kan den skrivas y = kx+m. Vi vet att tangenten ska gå genom punkten 0,2, alltså gäller att 2 = k*0+m, => m = 2
En tangent till funktionen 9-x2 har lutningen -2x.
Vårt k i tangentens ekvation är därmed -2x, och vi kan skriva tangentens ekvation som
Y = -2x2+2
Återstår att se om vi har en tangeringspunkt där -2x2+2 = 9-x2
förenklar vi får vi:
-7 = x2 som saknar lösning, alltså är svaret nej.
Men det hade varit mycket enklare att rita som Yngve rekommenderade
Ture, när du skriver att tangentens ekvation är y = -2x2 + 2
menar du väl bara sambandet mellan x och y i en eventuell tangeringspunkt.
Vilket ger ekvationen du skrev och som saknar lösning.
Ture skrev:svaret är nej, men jag tror inte att du har full koll på varför.
En tangent är en rät linje, alltså kan den skrivas y = kx+m. Vi vet att tangenten ska gå genom punkten 0,2, alltså gäller att 2 = k*0+m, => m = 2
hur kan man utifrån en punkt bestämma hur linjen ser ut? krävs inte det minst 2?
En tangent till funktionen 9-x2 har lutningen -2x.
Vårt k i tangentens ekvation är därmed -2x, och vi kan skriva tangentens ekvation som
Y = -2x2+2
men funktionens lutning var väl -2x bara? hur kan man utifrån ena linjens m-värde veta att denna funktion också har detta m-värde?
Återstår att se om vi har en tangeringspunkt där -2x2+2 = 9-x2
Här försöker man väl hitta gemensam punkt?
förenklar vi får vi:
-7 = x2 som saknar lösning, alltså är svaret nej.
Men det hade varit mycket enklare att rita som Yngve rekommenderade
jag visste inte hur jag skulle föra in punkten (0,2) i min miniräknare (eller nu när jag tänker efter hade jag kunnat kolla med "pil") så jag ritade in det i geogebra och fick följande
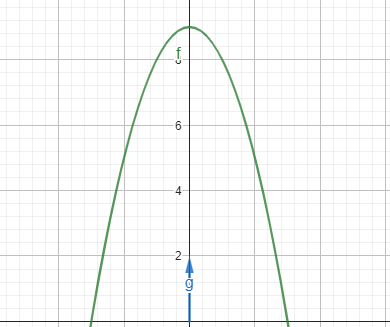
men det sa mig inte heller så mycket mer än att funktionen inte har en punkt där (alltså jag visste inte riktigt hur jag skulle redovisa mitt svar)
därför ville jag lösa det algebraiskt (dels för att lära mig men även för att vi inte får använda geogebra under prov)
Louis skrev:Ture, när du skriver att tangentens ekvation är y = -2x2 + 2
menar du väl bara sambandet mellan x och y i en eventuell tangeringspunkt.
Vilket ger ekvationen du skrev och som saknar lösning.
just det,
Jag var inte tillräckligt tydlig, tack för påpekandet!
naturnatur1 skrev:Ture skrev:svaret är nej, men jag tror inte att du har full koll på varför.
En tangent är en rät linje, alltså kan den skrivas y = kx+m. Vi vet att tangenten ska gå genom punkten 0,2, alltså gäller att 2 = k*0+m, => m = 2
hur kan man utifrån en punkt bestämma hur linjen ser ut? krävs inte det minst 2?
Jo det krävs 2 punkter för att bestämma både k och m, men i det här fallet kunde vi bestämma m, tack vare att x var 0 i den kända punkten
En tangent till funktionen 9-x2 har lutningen -2x.
Vårt k i tangentens ekvation är därmed -2x, och vi kan skriva tangentens ekvation som
Y = -2x2+2
men funktionens lutning var väl -2x bara? hur kan man utifrån ena linjens m-värde veta att denna funktion också har detta m-värde?
Funktionens lutning är -2x överallt, (den beror alltså av x) den tangent vi söker har ett, eller möjligen 2, värden på x, x-värdet är tangeringspunktens x-koordinat. (om vi hittar 2 värden på x så har vi två olika tangenter)
Återstår att se om vi har en tangeringspunkt där -2x2+2 = 9-x2
Här försöker man väl hitta gemensam punkt?
Ja
förenklar vi får vi:
-7 = x2 som saknar lösning, alltså är svaret nej.
Men det hade varit mycket enklare att rita som Yngve rekommenderade
jag visste inte hur jag skulle föra in punkten (0,2) i min miniräknare (eller nu när jag tänker efter hade jag kunnat kolla med "pil") så jag ritade in det i geogebra och fick följande
men det sa mig inte heller så mycket mer än att funktionen inte har en punkt där (alltså jag visste inte riktigt hur jag skulle redovisa mitt svar)
Kan du med hjälp av en penna och den geogebrafigur du tagit fram rita en tangent till kurvan som går genom (0,2)? Rita några tangenter till din gröna kurva, kan du hitta någon som går genom (0,2)?
därför ville jag lösa det algebraiskt (dels för att lära mig men även för att vi inte får använda geogebra under prov)
Inget fel med det, bra att kunna bägge metoderna!
Jag tycker du ska lära dig rita andragradskurvor utan hjälpmedel, tips:
- Det är alltid en parabel, negativt tecken framför x2 så blir det en ledsen mun annars glad.
- Bestäm nollställena (om de existerar, annars symmetrilinjen) och max/min sen är det lätt att rita.
så först hitta man alltså linjen till den givna punkten (0,2), vilket man enkelt kunde göra då x=0 (kan jag ha det som tumregel? alltså ifall jag ska hitta linje till en punkt med x-koordinaten 0 så är y-koordinaten m-värdet?)
(((hur hade man gjort om punkten var exempelvis (1,4?) )))
i detta fallet var det väl y= 2 , då x=0
förstår dock fortfarande inte riktigt hur man drog slutsatsen att den deriverade givna funktionen y= -2x helt "plötsligt" blev till y = -2x + 2
liksom vad är det som blev -2x+2, är det tangenten?
och varför sätter man
funktion = deriverade funktion?
(ja, för att hitta gemensam punkt, men förstår inte varför det är just de funktionerna)
ursäkta för frågorna men tycker att denna uppgift var luddig..(:
naturnatur1 skrev:så först hitta man alltså linjen till den givna punkten (0,2), vilket man enkelt kunde göra då x=0 (kan jag ha det som tumregel? alltså ifall jag ska hitta linje till en punkt med x-koordinaten 0 så är y-koordinaten m-värdet?)
Nej vi hittade inte någon linje till punkten, vi räknade ut m-värdet för alla linjer som går genom punkten 0,2. Man frågade ju efter en tangent som går genom den punkten och tangerar kurvan i en annan punkt.
(((hur hade man gjort om punkten var exempelvis (1,4?) )))
i detta fallet var det väl y= 2 , då x=0
Då hade vi fått 4 = k*1+m, alltså inget entydigt värde på m och den fortsatta bräkningen hade blivit bökigare men inte omöjlig.
förstår dock fortfarande inte riktigt hur man drog slutsatsen att den deriverade givna funktionen y= -2x helt "plötsligt" blev till y = -2x + 2
liksom vad är det som blev -2x+2, är det tangenten?
Den tangent vi söker ska ha en lutning som är lika med funktionens derivata i tangeringspunkten. Vi känner inte till vilket x-värde en ev tangeringspunkt har, men vi vet att om den existerar har den lutningen -2x, där x är tangeringspunktens x-värde.
tangentens ekvation blir då y = kx+2, där k = -2x, vilket alltså blir y = -2x2+2
och varför sätter man
funktion = deriverade funktion?
(ja, för att hitta gemensam punkt, men förstår inte varför det är just de funktionerna)
ursäkta för frågorna men tycker att denna uppgift var luddig..(:
Vår sökta tangent har en punkt gemensam med kurvan därför måste y-värdena vara lika så vi kan sätta
t(x) = f(x) dvs tangenten = funktionen i för ett visst värde på x
därav -2x2 +2 = 9-x2
Det blir mycket lättare att förstå, och därmed göra rätt, om man först ritar.
Prova gärna om du kan hitta en tangent till din funktion om tangenten ska gå genom (0,13)