Tangens-ekvation

Hej,

Jag försöker lösa uppgiften tan 3x = tan x, men lyckas inte riktigt. Här är en beskrivning av hur man bör tänka:

Jag är med på det första resonemanget, men jag hänger inte med då man försöker visa vid vilka x som cosinus är noll, mer specifikt just denna likhet:

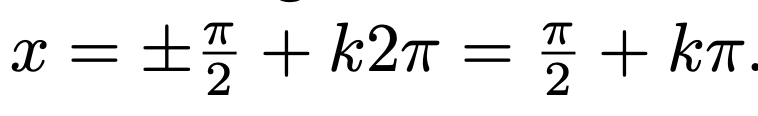
Vad händer med 2:an som multipliceras med k och pi? Och varför försvinner den negativa "roten"?

Hej.

Markera de två lösningsmängderna

$x=\pm\frac{\pi}{2}+k2\pi$ och $\cancel{x=\frac{\pi}{2}+2\pi}$ I enhetscirkeln.

Ser du då att de sammanfaller?

=========

EDIT - Andra lösningsmängden ska vara $x=\frac{\pi}{2}+k\cdot\pi$

Tack Laguna för påpekandet.

Yngve skrev:
Hej.

Markera de två lösningsmängderna

$x=\pm\frac{\pi}{2}+k2\pi$ och $x=\frac{\pi}{2}+2\pi$ I enhetscirkeln.

Ser du då att de sammanfaller?

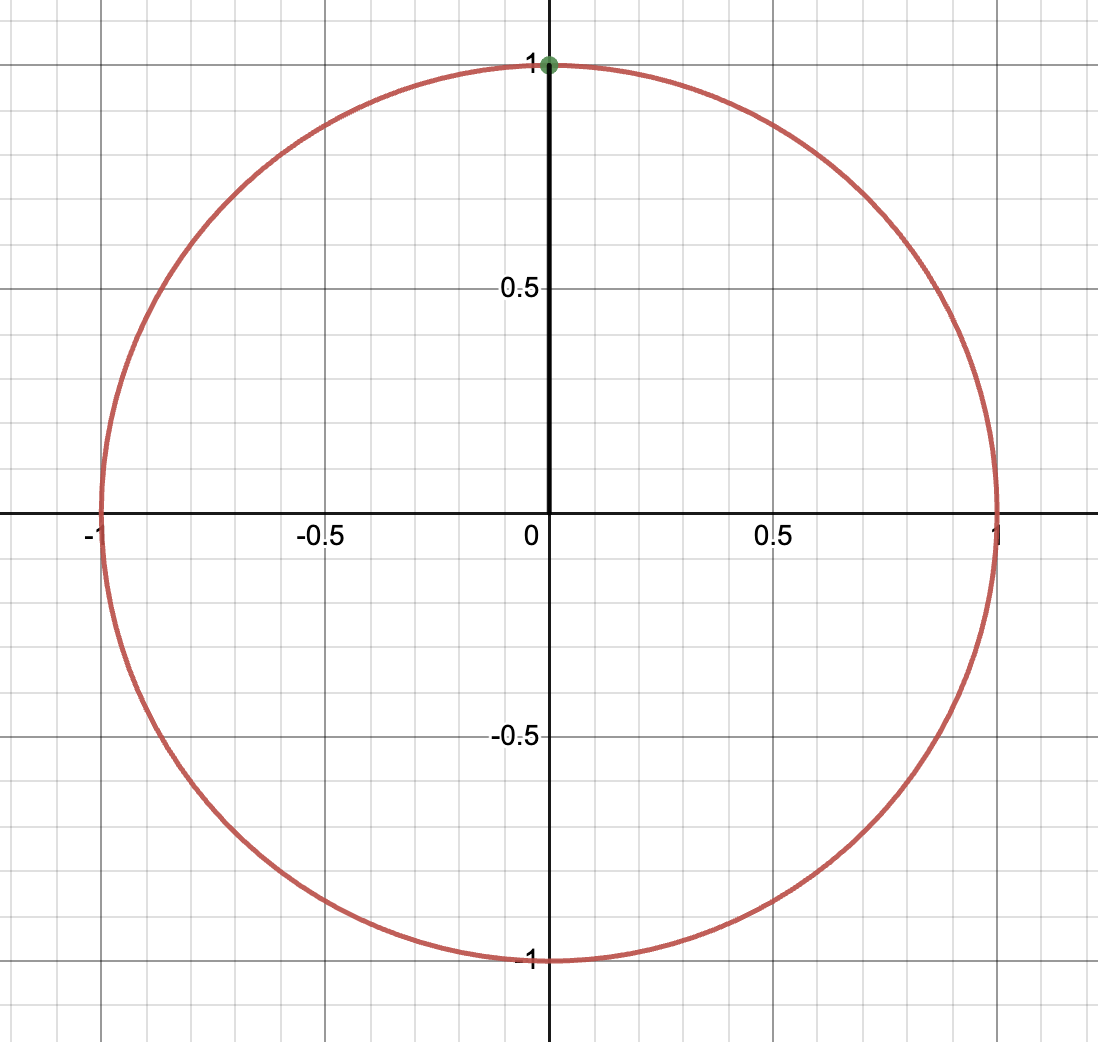I bilden ovan är x = pi/2, vilket kommer vara odefinierat för tangens.
Hade jag målat punkten för x = -pi/2 så hade den punkten varit längst ned i cirkeln (-90 grader).
För mig känns det som omskrivningen till x = pi/2 + 2pi missar lösningar på nedre halvan av enhetscirkeln?

Jag är med på att funktionen inte är definierad för dessa värden på x. Men hur kommer man då fram till lösningen x = k * pi? Hur kan man dra den slutsatsen?

starboy skrev:
För mig känns det som omskrivningen till x = pi/2 + 2pi missar lösningar på nedre halvan av enhetscirkeln?

Förlåt jag skrev fel, det ska vara pi/2 + k*pi.

Då finns lösningarna på nedre halvan med.

Jag är med på att funktionen inte är definierad för dessa värden på x. Men hur kommer man då fram till lösningen x = k * pi? Hur kan man dra den slutsatsen?

Se uppdaterat svar #2

Svara

Visa senaste svar