Tangens
Varför ser tangenskurvor ut som de gör?
Bestäm tan(x) för några värden mellan 0 och 2π (eller 0° och 360°).
Markera (x, tan(x)) för dessa punkter i ett koordinatsystem.
eller
Rita en enhetscirkel + [den lodräta linjen x = 1]
Dra en linje genom origo så att den skär cirkeln i två punkter
och [den lodräta linjen x = 1] i en punkt.
Den sistnämnda skärningspunktens y-koordinat är tan(x) för
de båda vinklar som markeras av de två punkter
där linjen genom origo så skär cirkeln.
(svårt i ord, lätt att rita!)
Ta ett varv i enhetscirkeln och notera hur tan(x) varierar.
Arktos skrev:Bestäm tan(x) för några värden mellan 0 och 2π (eller 0° och 360°).
Markera (x, tan(x)) för dessa punkter i ett koordinatsystem.eller
Rita en enhetscirkel + [den lodräta linjen x = 1]
Dra en linje genom origo så att den skär cirkeln i två punkter
och [den lodräta linjen x = 1] i en punkt.
Den sistnämnda skärningspunktens y-koordinat är tan(x) för
de båda vinklar som markeras av de två punkter
där linjen genom origo så skär cirkeln.(svårt i ord, lätt att rita!)
Ta ett varv i enhetscirkeln och notera hur tan(x) varierar.
Tack, jag testade göra det.
Om jag har ekvationen tan2x = 0,9
Hur vet jag hur många lösningar den kommer att få inom intervallet 0⁰ ≤ v ≤ 360⁰?
Är inte så bekväm med tangenskurvan än, så vet inte hur jag ska se det.
Vilka vinklar har tangens lika med 0,9 ?
Kolla i figuren.
Om den ena är x° så är den andra mitt emot i cirkeln.
Arktos skrev:Vilka vinklar har tangens lika med 0,9 ?
Kolla i figuren.
Tan-1(0,9) =
X = 42⁰ + n × 180⁰
Tan2x = 0,9 blir samma fast dividerat med 2, alltså
X = 21⁰ + n × 90⁰
Om den ena är x° så är den andra mitt emot i cirkeln.
Hur menar du?
Åter till figuren i #3
Dra en linje genom origo så att den skär [den lodräta linjen x = 1] i punkten (1; 0.9)
och cirkeln i två punkter.
Dessa två punkter anger de två vinklar, för vilka tangens är lika med 0,9
i intervallet [0°, 360°].
Arktos skrev:Åter till figuren i #3
Dra en linje genom origo så att den skär [den lodräta linjen x = 1] i punkten (1; 0.9)
och cirkeln i två punkter.Dessa två punkter anger de två vinklar, för vilka tangens är lika med 0,9
i intervallet [0°, 360°].
Det finns ingen figur i själva frågan. Ska jag skapa en mha miniräknare? Eller går det utan?
Vad ger miniräknaren för värde på arctan(0,9) ?
Nu "skriver vi om" varandra.
Mittemot är 180° bort (rita!)
dvs 42° och 222° (båda på linjen genom origo)
Arktos skrev:Vad ger miniräknaren för värde på arctan(0,9) ?
≈ 42⁰
Jag vet dock inte riktigt hur jag ska rita det. Jag ser dock att tan(42) och tan(222) hamnar på samma värde (y)
Dra en linje genom origo
så att den skär [den lodräta linjen x = 1] i punkten (1; 0.9).
Den har både vinkeln ca 42° mot positiva x-axeln
och vinkeln ca 42°+180° = 222° mot positiva x-axeln.
naturnatur1 skrev:Tan-1(0,9) =
X = 42⁰ + n × 180⁰
Tan2x = 0,9 blir samma fast dividerat med 2, alltså
X = 21⁰ + n × 90⁰
dvs 2x = 42 + n*180 där n är ett godtyckligt heltal
och x = 21 + n*90 där n är ett godtyckligt heltal
Frågan är vilka av dessa värden på x som ligger mellan 0 och 360 .
Jag hänger inte riktigt med på rit delen om jag ska vara ärlig, för jag fattar inte riktigt vad det är jag ska se (jo, skärningen, men inte hur jag ska se det typ) och detta förstår jag inte riktigt heller:
Den har både vinkeln ca 42° mot positiva x-axeln
och vinkeln ca 42°+180° = 222° mot positiva x-axeln.
Det här begriper jag dock:
dvs 2x = 42 + n*180 där n är ett godtyckligt heltal
och x = 21 + n*90 där n är ett godtyckligt heltal
Frågan är vilka av dessa värden på x som ligger mellan 0 och 360 .
21⁰ , 111⁰, 201⁰ , 291⁰.
Det räcker att du "ser" det på det sista sättet.
Den geometriska lösningen kan vara svår att se utan att rita figuren,
men har man ritat och "sett", glömmer man den inte :-)
Det är en fördel att kunna behandla en uppgift både geometriskt och algebraiskt.
Gör man "fel" på det ena sättet kan man pröva det andra.
Passa på att öva båda sätten, där det går .
Arktos skrev:Det räcker att du "ser" det på det sista sättet.
Den geometriska lösningen kan vara svår att se utan att rita figuren,
men har man ritat och "sett", glömmer man den inte :-)Det är en fördel att kunna behandla en uppgift både geometriskt och algebraiskt.
Gör man "fel" på det ena sättet kan man pröva det andra.
Passa på att öva båda sätten, där det går .
Skulle du kunna hjälpa mig att se det genom figuren/bild/ritningen? Jag har enklare för att se det algebraiskt men vill gärna även kunna se detta geometriskt (:
Den borde stå i kursboken, men ofta nöjer man sig nog med bara enhetscirkeln.
Den räcker för uppgifter med sinus eller cosinus.
Vill man även "se" tangens, räcker det med att tillfoga den lodräta linjen x = 1 .
dvs tangenten till cirkeln genom (1, 0).
Exempel
Dra en linje genom (0, 0) och (1, 1). Den lutar 45° , k-värde = 1
Den punkt där den skär cirkeln har därför koordinaterna (cos(45°), sin(45°))
Linjen har därför lutningen sin(45°)/cos(45°) = tan(45°)
och skär därför den lodräta linjen i (1, tan(45°)) = (1, 1).
Fortsätt själv med att t ex dra en 60-graders linje genom origo
och förvissa dig om att den skär den lodräta linjen i (1, tan(60))
därför att den har lutningen sin(60°)/cos(60°) = tan(60°)
Rita! Kanske inte nu, men vid lämpligt senare tillfälle...
naturnatur1 skrev:Skulle du kunna hjälpa mig att se det genom figuren/bild/ritningen? Jag har enklare för att se det algebraiskt men vill gärna även kunna se detta geometriskt (:
Jag hittade en animation på den tyska wiki-sidan om enhetscirkel.
https://de.wikipedia.org/wiki/Einheitskreis#/media/Datei:Einheitskreis_Ani.gif
Funkar den?
Nästa bild är en stillastående variant, där
• den rosa sträckan är sin(φ)
• den gröna sträckan är cos(φ)
• den blåa sträckan är tan(φ)
Tack! @Arktos
Har du möjlighet att bifoga bild på din ritning? Hur ska jag se exempeluppgiften (tan2x= 0,9) geometriskt? Jag kan se den i miniräknaren men jag vet inte hur man ska gå tillväga om man vill rita grafen? (Eller om det ens behövs?)
Ja, länkarna du bifogade funkar!
Jag repeterar (se #11):
• Rita en enhetscirkel och dra (den lodräta) linjen x = 1 .
• Dra en linje genom origo och punkten (1; 0.9) (på den lodräta linjen)
• Den skär cirkeln i två punkter och har därför
både vinkeln ca 42° och vinkeln ca 42°+180° = 222°
mot positiva x-axeln
Rita denna figur! (Visa den gärna här i tråden)
Den ger sambandet 2x = ca 42° + n*180°
och lösningen x = ca 21° + n*90° (se #12, 13)
Jämför din figur med den i den undre länken i #17.
Vitsen med detta är att du ska se
att du även kan lösa uppgiften "geometriskt".
(se #14, 15)
Arktos skrev:Jag repeterar (se #11):
• Rita en enhetscirkel och dra (den lodräta) linjen x = 1 .
• Dra en linje genom origo och punkten (1; 0.9) (på den lodräta linjen)
Varför sätter man 0,9 som y värdet?
• Den skär cirkeln i två punkter och har därför
både vinkeln ca 42° och vinkeln ca 42°+180° = 222°
mot positiva x-axeln
Varför är den andra punkten (222⁰) nödvändig att ha med?
Rita denna figur! (Visa den gärna här i tråden)
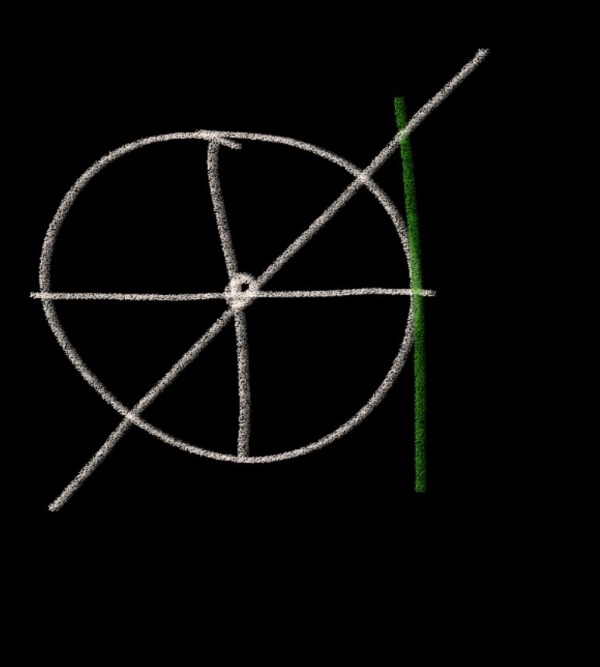
(Jätte slarvig och tråkig men ungefär så)
Den ger sambandet 2x = ca 42° + n*180°
och lösningen x = ca 21° + n*90° (se #12, 13)Jämför din figur med den i den undre länken i #17.
Vitsen med detta är att du ska se
att du även kan lösa uppgiften "geometriskt".
(se #14, 15)
Hänger tyvärr inte riktigt med på hur jag ska se lösningen:/ kan du visa hur du gör, tror det blir enklare
Tillägg: 20 sep 2023 21:03
Jag ser lösningen för tanx=0,9
Men hur ser man tan2x = 0,9
Bra figur!
sätt ut vinklarna också
Och gärna x och y på koordinataxlarna.
och 1 där cirkeln tangerar linjen x=1 .
och koordinaterna där linjen genom origo skär den lodräta tangenten.
Hur mycket du behöver sätta ut, beror förstås på till vem du vänder dig.
Som skiss för egen del räcker det väl att sätta ut (1, 0,9)
och de två vinklarna.
Arktos skrev:Bra figur!
sätt ut vinklarna också
Och gärna x och y på koordinataxlarna.
och 1 där cirkeln tangerar linjen x=1 .
och koordinaterna där linjen genom origo skär den lodräta tangenten.
Hur mycket du behöver sätta ut, beror förstås på till vem du vänder dig.
Som skiss för egen del räcker det väl att sätta ut (1, 0,9)
och de två vinklarna.
Jag gjorde det nu. Men jag fattar inte riktigt varför x blir 1 och y blir 0,9
Det står dock 2x, ska jag dela vinklarna på 2? (I mitten?)
Om vinkeln är v så skär [linjen genom origo]
den lodräta [linjen x=1] i punkten (1, tan(v))
Det blir trassligt när vinklar och koordinataxlar har samma beteckningar.
Du ville lösa ekvationen tan(2x) = 0,9.
Då kan du lika gärna lösa ekvationen tan(2v) = 0,9
Kalla vinkeln i figuren för 2v så är saken klar
[linjen genom origo] skär då den lodräta [linjen x=1]
i punkten (1, tan(2v))
så 2v = arctan(0,9) + n*180°
och v = [arctan(0,9)]/2 + n*90° precis som tidigare, #19,
där 42° var ett närmevärde till arctan(0,9)
Mycket att hålla reda på!
Tillägg: 21 sep 2023 14:59
Här är en figur, snabbt framställd i Desmos

Tack så mycket för hjälpen Arktos!

