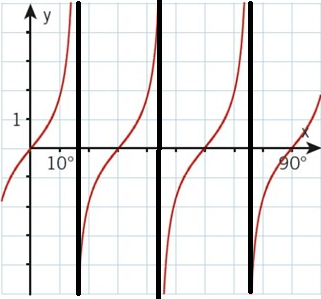
tan x asympytot

Den här grafen är inte $\tan x$. $\tan x$ är odefinierad för bl.a 90 grader och har en asymptot där.

naytte skrev:

Den här grafen är inte $\tan x$. $\tan x$ är odefinierad för bl.a 90 grader och har en asymptot där.

konstigt...boken säger att det är grafen till tan x. Här är frågan till grafen:

Ah, $\tan kx$, inte $\tan x$. Angående frågan med asymptoten:

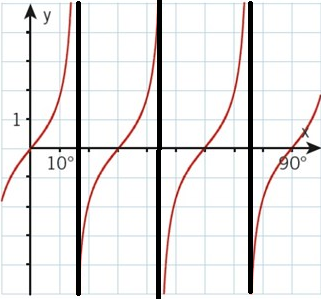
Där har du asymptoterna i den här kurvan. Asymptoterna dyker upp där $\cos kx = 0$, alltså $\displaystyle x =\frac{1}{k}(90 ^\circ+180^\circ n)$

Hodlys skrev:

naytte skrev:

Den här grafen är inte $\tan x$. $\tan x$ är odefinierad för bl.a 90 grader och har en asymptot där.

konstigt...boken säger att det är grafen till tan x. Här är frågan till grafen:

sin(kx)=0 då kx=180°n, n heltal.

n=1 , x=30° ger k=6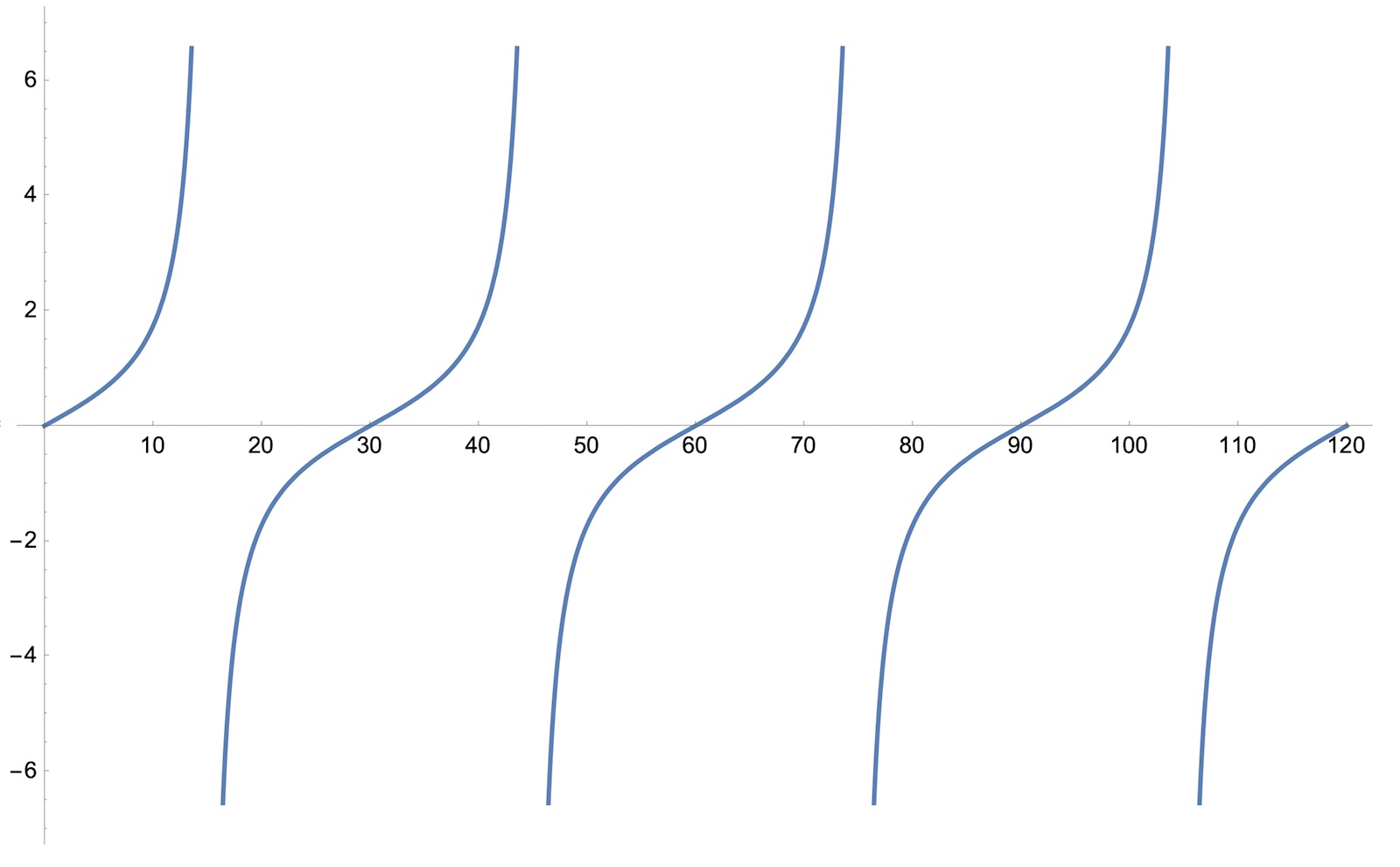

naytte skrev:

Ah, $\tan kx$, inte $\tan x$. Angående frågan med asymptoten:

Där har du asymptoterna i den här kurvan. Asymptoterna dyker upp där $\cos kx = 0$, alltså $\displaystyle x =\frac{1}{k}(90 ^\circ+180^\circ n)$

Finns det någon skillnad på hur grafen ser ut för tan(kx) i jämförelse med tan(x), men hur visste ni var asymptoterna befann sig?

Asymptoterna är där som kurvan aldrig riktigt kommer fram till, d v s varken de gula eller gröna linjerna du har ritat in är asymptoter, eftersom de skär kurvorna. Om du förklarar varför du har ritat dina linjer just där de är, kan vi nog hjälpas åt och komma fram till var du tänkte fel.

Hodlys skrev:

Finns det någon skillnad på hur grafen ser ut för tan(kx) i jämförelse med tan(x), 

Ja, det är skillnad.

Om k t.ex. är lika med 2 så blir uttrycket tan(2x) och grafen ser då ut så här:

Om k istället är lika med 3 så blir uttrycket tan(3x) och grafen ser då ut så här:

Om k istället är lika med 5 så blir uttrycket tan(5x) och grafen ser då ut så här:

Smaragdalena skrev:

Asymptoterna är där som kurvan aldrig riktigt kommer fram till, d v s varken de gula eller gröna linjerna du har ritat in är asymptoter, eftersom de skär kurvorna. Om du förklarar varför du har ritat dina linjer just där de är, kan vi nog hjälpas åt och komma fram till var du tänkte fel.

Om ni kollar på kurva 1 alltså den kurvan som skär i origo, tänkte jag att den kommer ju växa vilket gör att kurvan kommer närma sig mer min gula linje. 

Om du ritar den gula linjen vid 15 grader i stället för 20 så blir det bättre.

Yngve skrev:

Hodlys skrev:

Finns det någon skillnad på hur grafen ser ut för tan(kx) i jämförelse med tan(x), 

Ja, det är skillnad.

Om k t.ex. är lika med 2 så blir uttrycket tan(2x) och grafen ser då ut så här:

 

Så om jag ritar asymptoterna till kurvan tan(2x) får jag:

lol asymptoterna blev lite snea...

men om vi säger att jag inte visste vad k var i funktionen. Hur skulle jag fått  reda på det då?

men om vi säger att jag inte visste vad k var i funktionen. Hur skulle jag fått reda på det då?

Du vet (eller kan slå upp) att funktionen y = tan(1x) har perioden 180^o, d v s när x har gått från 0 till 180 så börjar funktionen om igen. Om vi istället har funktionen y = tan(2x) så räcker det att x går från 0 till 90 för att 2x skall gå från 0 till 180, d v s att funktionen börjar om igen. Om y = tan(10x) så räcker det att x går frn 0 till 18 för att funktionen skall börja om.

Ifall det råder ett missförstånd om vad en asymptot är: en kurva ska inte bara komma närmare och närmare asymptoten, den ska komma hur nära som helst.

En asymptot behöver inte heller vara en linje utan kan egentligen vara vilken typ av funktion som helst. Men komplexa (inte i den matematiska bemärkelsen!) asymptoter är inte så användbara.