Talet e
Fråga:
https://gyazo.com/896e991ad1f170cf5392520ac0832065
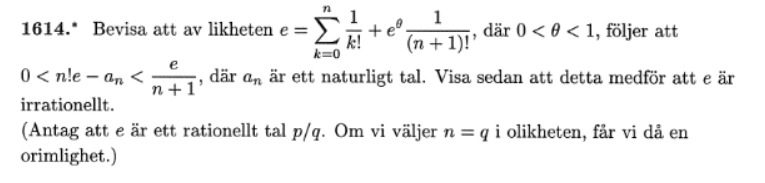
Mitt försök:
Jag vet inte riktigt hur jag ska tänka..
All hjälp på traven uppskattas!
Tog bort bilden på trådstartarens begäran - berräkningarna finns i ett inlägg längre ner i tråden. Fixade nivån ocklså. /Smaragdalena, moderator
Flyttade din tråd från forumdelen Bevis, som endast är avsett för färdiga bevis, inte för uppgifter du behöver hjälp med, till Ma3 där man lär sig om talet e. Är nivån fel, kan du själv flytta tråden genom att redigera förstainlägget (inom två timmar, efter det behöver du be en moderator om hjälp). /moderator
Smaragdalena skrev:Flyttade din tråd från forumdelen Bevis, som endast är avsett för färdiga bevis, inte för uppgifter du behöver hjälp med, till Ma3 där man lär sig om talet e. Är nivån fel, kan du själv flytta tråden genom att redigera förstainlägget (inom två timmar, efter det behöver du be en moderator om hjälp). /moderator
Det löste sig!
Ojoj det här är verkligen inte matte3
Qetsiyah skrev:Ojoj det här är verkligen inte matte3
Det har du verkligen rätt i, men tråden hör inte hemma i Bevis, och jag flyttade tråden innan jag la in bilden i frågan- då fanns det bara en länk. /moderator
nu blir jag nyfiken, vad pluggar du blygummi?
Qetsiyah skrev:nu blir jag nyfiken, vad pluggar du blygummi?
Hej! Det är en kurs i analys.
Men fann möjligtvis lösningen tror jag.. för dom intresserade:
Så, om man fokuserar på det som vi av frågan vet gäller:
Subtrahera över första termen i högerledet till vänsterledet och skriv sätt en övre begränsning av vänsterledet med hjälp av att begränsa theta, så att den går mot ett, dock så är theta inte definierad för theta = 1, i vilket fall går det att göra en sådan begränsning. När den gjorts är det bara att multiplicera med n! i respektive led så är man i mål, skulle jag tro.
Dock återstår att visa att det medför att e då är irrationellt.
Visa spoiler
Det du har här är i princip Fouriers bevis för att e är irrationellt. Det finns dokumenterat på wikipedia: https://en.wikipedia.org/wiki/Proof_that_e_is_irrational#Fourier's_proof




