Svårt med att se den motsatta sidan
Hej, jag ska lösa y & x sida. Hos triangeln. Så här ser den ut:
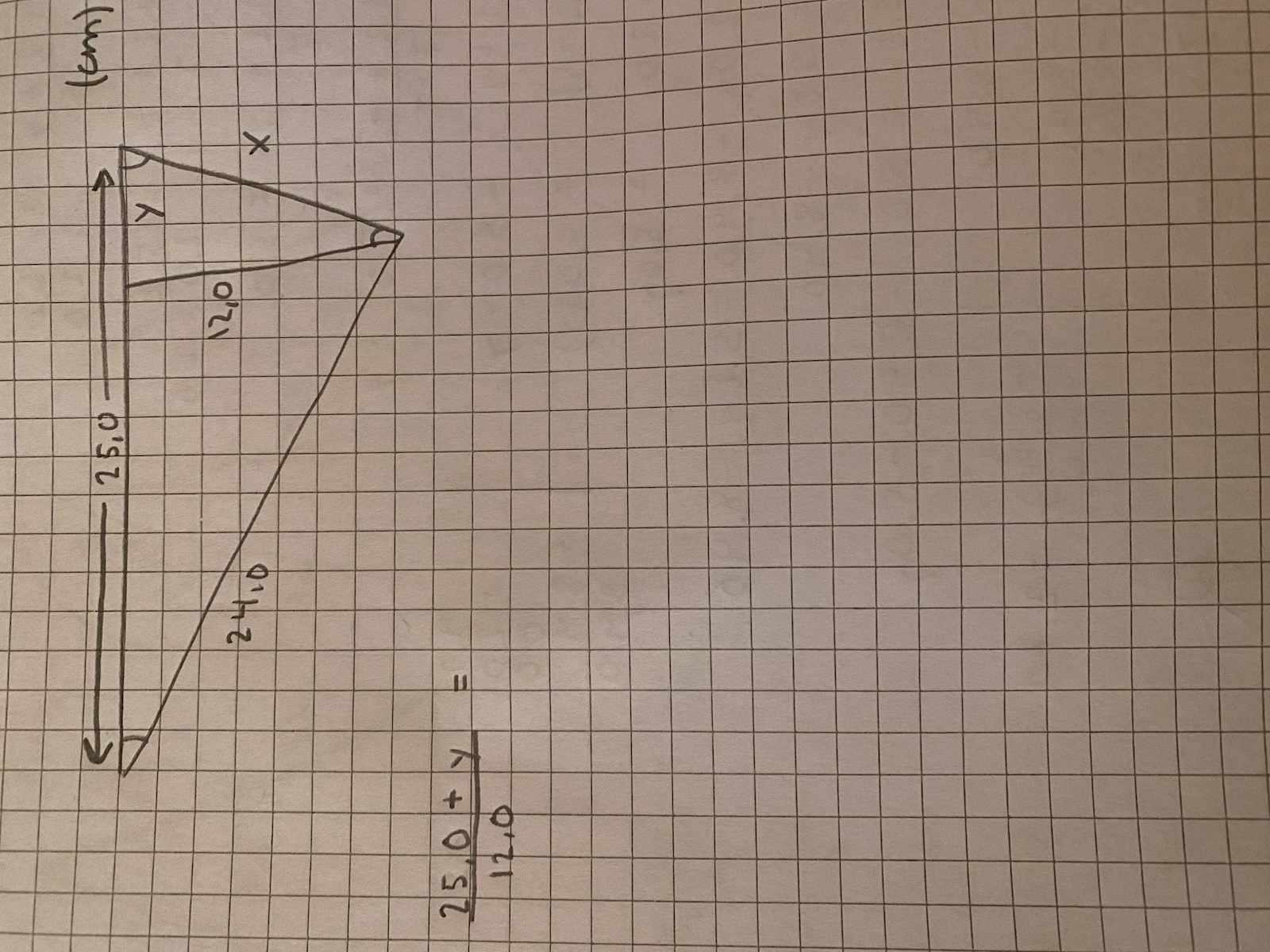 försöker se den motsatta sidan till trianglarna.
försöker se den motsatta sidan till trianglarna.
den lilla triangelns y sida blir den stora triangelns x som motsatt sida. Det går väl inte?
tänker att sidan 25.0 + y har sin motsatta sida 12.0 & inte x? Detta då jag bara vill ha en obekant i ekvationen.
men sen kan ju 24.0 sidan hos den stora triangeln inte ha motsatt sida av den lilla triangeln x det blir ju en konstig ekvation då?
hur gör man?
Är 12,0 höjden? Dvs den är vinkelrät i så fall mot basen 25,0. Fundera vilka villkor som behövs för likformighet.
Tack för svaret. Det står att " för att bevisa att triangeln är likformig måste man antingen visa att vinklarna i triangeln är lika stora eller att förhållandet mellan motsvarande sida är lika"
Eftersom att trianglarna inte har någon hake utan bågar så tror jag inte de är 90 grader.
och jag kan inte lösa uppgiften för jag vet inte hur jag får motsatt sida utan att få in 2 obekanta i ekvationen?
Ska jag kanske försöka lösa uppgiften med hjälp av vinklarna?
En triangel är ju 180 grader.. men hur får jag reda på x sida och y sida med hjälp av vinklarna?
Så här ser den ut:
Det har markerats i figuren att att den minsta triangeln har lika stora vinklar som den stora.
De är alltså likformiga.
hej, okej tack. Men liksom hur ser du det? vet du det? räkna du fram det?
Du kan se att triangel ACD är lilformig med triangel BCD på följande sätt:
- Båda trianglarna selar vinkel vid C, alltså har de lila stora vinklar där.
- Vinkeln vid A i triangel ACD är lika stor som vinkeln vid D i triangeln BCD. Detta framgår av att det är ett streck på vinkelnarkeringen på båda ställena.

okej, tack. Men jag förstår inte hur jag få fram y och x utifrån denna info?
Ska jag kanske försöka få fram x och y med hjälp av skala? fast det går ju inte heller..
facit säger: x = 12,5 cm, y = 6,25 cm
Naturens skrev:okej, tack. Men jag förstår inte hur jag få fram y och x utifrån denna info?
Ska jag kanske försöka få fram x och y med hjälp av skala? fast det går ju inte heller..
facit säger: x = 12,5 cm, y = 6,25 cm
Likformighet. Tips: rita upp de båda trianglarna så att de är vridna åt samma håll, så är det enklare att se vilka sidor som motsvarar varandra.
jo men blir osäker på om den lila triangeln kanske är typ spegelvänd eller något sånt också, då liksom blir de ju fel ändå?, men ska försöka och se
Jag gjorde så här
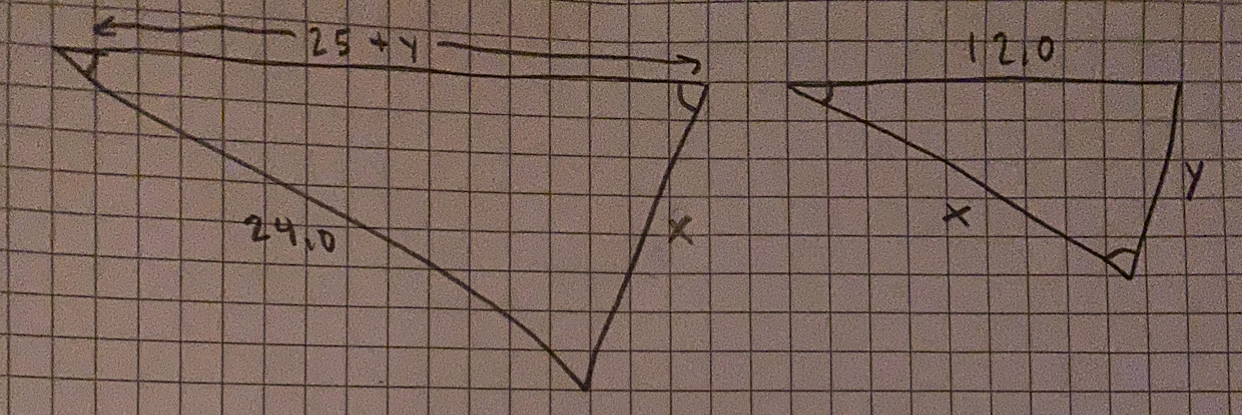
På den stora vill jag typ skriva 12,0 för jag tycker dom sidorna ser lika stora ut men det vet man ju inte. Så jag skrev x där med för det är ju ”tomt” där?
Så här blir figurerna. Det gäller att se hur du ska vända på den lilla triangeln.
Sidan som står mitt emot vinkeln vid C (med två streck) är 12 cm i den lilla triangeln och 24 cm i den stora.
Det är alltså sidor som motsvarar varandra.

Här ser du att du genast kan få ut x (med huvudräkning).
Naturens skrev:jo men blir osäker på om den lila triangeln kanske är typ spegelvänd eller något sånt också, då liksom blir de ju fel ändå?, men ska försöka och se
Det är precis för att kunna upptäcka sådant som man ritar. Det är mycket svårare att upptäcka "i huvudet".
Oj då, ja just det. Tack igen, ska se om jag kan lösa denna uppgift nu : )
Ja, den är spegelvänd.
Då kan det vara svårt att se vilka sidor som hänger ihop med vilka i de två trianglarna.
Hör kommer ett tips för att reda ut det:
Utgå från det gemensamma hörnet C.
I den stora triangeln ACD: :Följ sidan AC (med längden 25,0 cm) till hörnet A, där vinkeln med ett streck på vinkelmarkeringen finns.
I den lilla triangeln BCD: Följ sidan CD (med längden x) till hörnet B, där vinkeln med ett streck på vinkelmarkeringen finns.
Dessa två sidlängder (25,0 cm och x) hänger alltså ihop.
Försök nu att på liknande sätt se vilka övriga sidlängder som hänger ihop.
Lyckades lösa uppgiften till slut. Har svårt att se ibland och veta hur jag ska vända triangeln. Sen är det svårt att veta hur man ställer upp ekvationerna ibland, då vissa uppgifter vill att man tar med, ex y i en uträkning ( ex 25,0 + eller - y). Men det gick till slut. TACK för tipsen. Skrev upp dom i mitt häfte under uppgiften så jag kommer ihåg allt sen när jag räknar om den här uppgiften (eller liknande).



