Svårt att tolka text uppgift, osäker på hur jag ska tänka & att jag tänker fel

Naturens skrev:

Hej, 

Har en textuppgift som är: 
I slutet av 2000 bodde 71.652 personer i Luleå kommun. I slutet av 2010 hade befolkningen ökat till 74.172 personer. Ökningen antas ske exponentiellt. När kommer befolkningen i Luleå kommun att överstiga 80.000 personer?

Jag har gjort liknande uppgifter förr, men den här är krångligare (tycker jag) för det är liksom 3 saker att hålla koll på och inte bara 1 sak att liksom ta reda på..

Jag tänker: 

År 2000 bodde 71.652 personer där 
År 2010 bodde 74.172 personer där 
Vilket år bor det 80.000 personer där 

Jag har formeln=  y= C*a^x.    där c= värdet, a=förändringsfaktorn och x= år 

Jag vill veta vilket år det är 80.000 personer som bor där. & detta med hjälp av formeln.. 

Ska jag göra två olika ekvationer:
En med värdena: År 2000 bodde 71.652 personer. 
En annan med.   :År 2010 bodde 74.172 personer . 
och försöka få fram a värdet från dessa två, dvs ff som jag sen gör om till %. 
Jämföra skillnaden mellan dessa i % och sätta in det värdet jag får i en tredje och ny ekvation med:

värde 80.000 på C
med den "nya %" som jag fått från de andra två ekvationerna, och göra om % till FF och placera in den FF på a platsen för att sedan frösöka få fram x värdet som då ska vara år. & på de viset få fram vilket år det är 80.000 personer? 

Det känns jätte bökigt och typ långt och jobbigt och fel.. men de är typ de enda jag kan komma på?

typ

Ekvation 1: 
71652*a^2000.   vad är a? få fram ff, gör om ff till %

Ekvation 2: 
74172*a^2010.    vad är a? få fram ff, gör om ff till %

Ta procenterna typ - varandra och få fram skillnaden 
Ta den skillnaden i % och gör om till ff och stoppa in i:

Ekvation 3:
80000 * (ff skillnaden mellan de två ekvationerna ovan)^x försök få fram året

Du kan göra det på det sätt som du beskriver, men det är onödigt komplicerat. Gör så här istället:

Sätt att t = 0 år 2000. Då blir den första ekvationen 71 652 = C^.a⁰, d v s C = 71 652. År 2010 är t = 10, så nästa ekvation är 74 172 = 71 652^.a¹⁰. Använd denna ekvation för att ta fram värdet på a. Sätt in värdena på C och a i ekvationen 80 000 = Ca^t och beräkna t.

@Naturens

Kolla också din förra uppgift, den om sälarna
Nu är det folk i stället  :-)
https://www.pluggakuten.se/trad/vill-ha-1-obekant-och-inte-2-i-ekvationen-hur-tanker-man/

Tack för svaren. 

Jag gjorde så här att jag tog fram a) med hjälp av räknare men jag får använda räknare på den här uppgiften.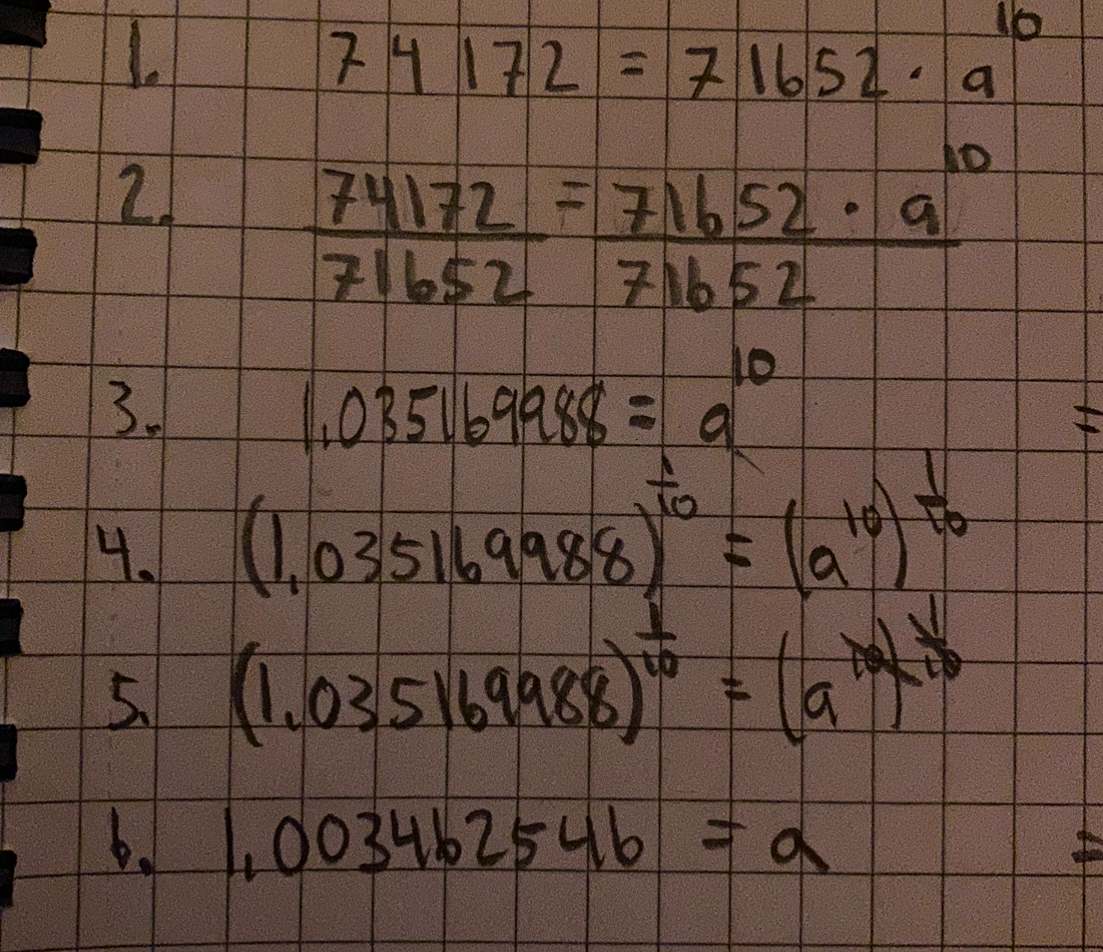 

sen tog jag hela a & gjorde en ny ekvation för att försöka få fram året så här:

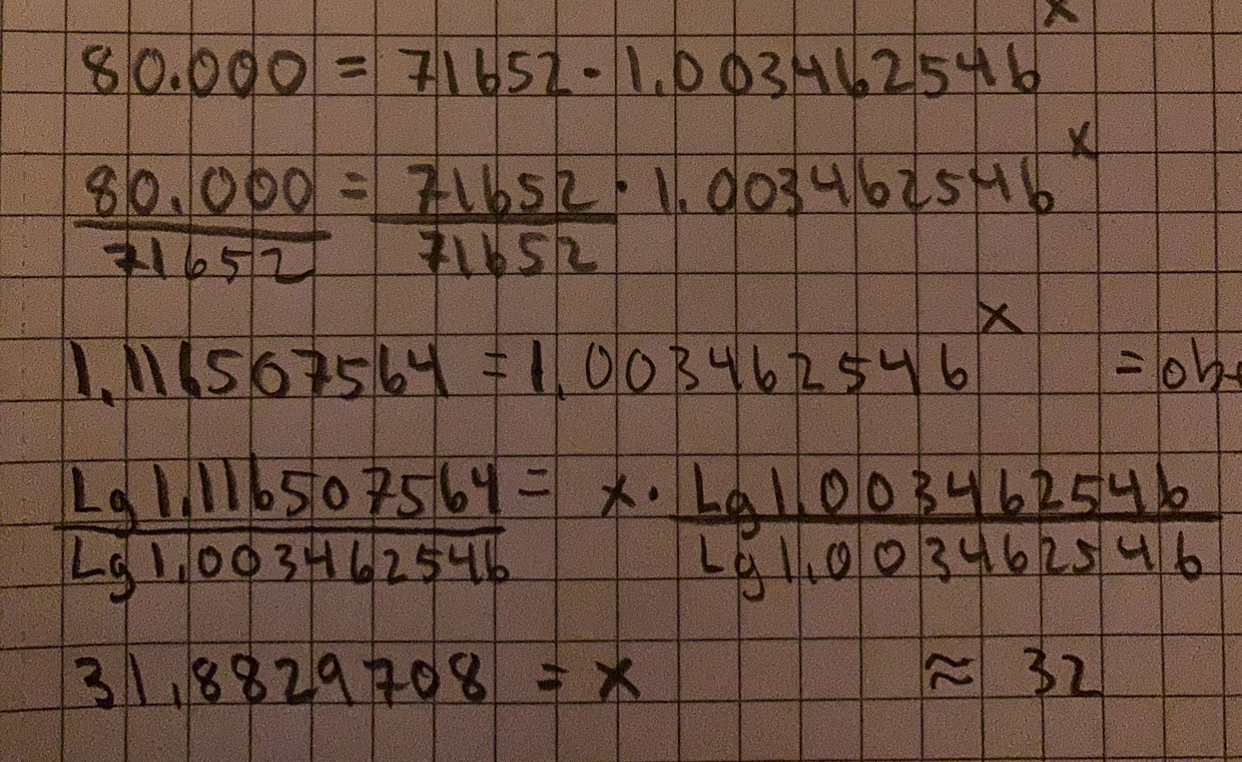sen gjorde jag så här:

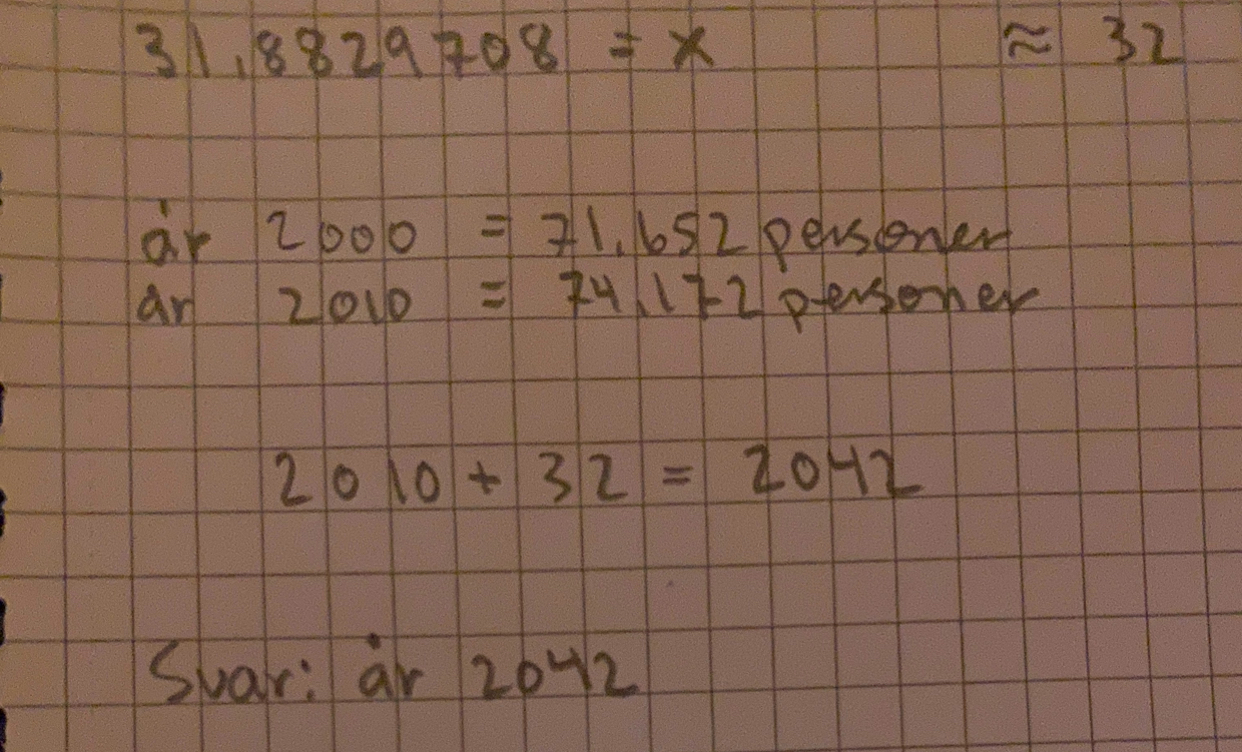har jag räknat rätt? 

har jag räknat rätt?

Nästan! Det ser bra ut ända tills sista rutan. Vilket år var det 71 652 invånare? Det var 32 år efter detta årtal som det kommer att vara 80 000 invånare i Luleå, om modellen stämmer.

jaha okej, så jag räknar då från 
år 2000 + 32 = år 2032 ?

Ja.