svår uppgift: ljusstråle riktat mot ett glasprisma
Hej alla på pluggakuten!
Jag har stirrat mig blind på en svår uppgift och kommer inte vidare. All hjälp mottas tacksamt!
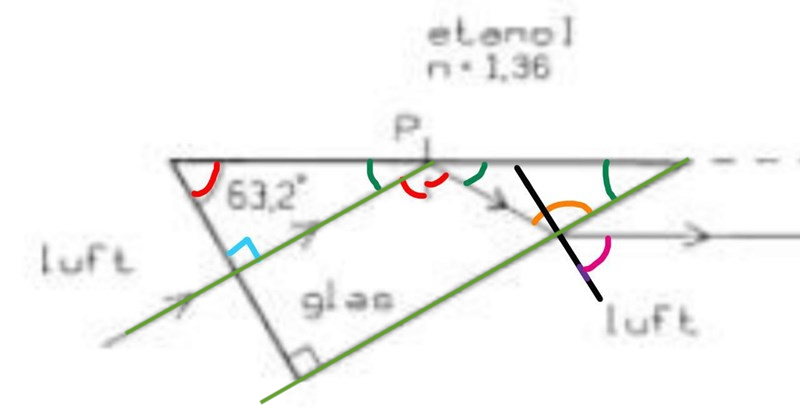
Uppgiften är som så att en ljusstråle skjuts mot ett glasprisma som omges av etanol på ena sidan och luft på de övriga två sidorna (se bild 1). Man ska undersöka om det finns ett ett värde på glasets brytningsindex som gör att inget ljus tränger in i etanolen vid punkten P och strålen lämnar prismat parallellt med gränsytan mot etanolen. Om det finns ett värde ska man dessutom ange det.
Bild 1.
Så här tänker jag (se bild 2):
a = 180°-63,2° = 26,8°
Eftersom a och b är alternatvinklar så borde a = b = 26,8° (se bild 2). Eftersom triangeln PRS är likbent så borde två av vinklarna vara 26,8°.
Därför måste c = 90° - a = 90°-28,8° = 65,2°
Bild 2.
Eftersom ljuset totalreflekteras tillbaka ner i prismat istället för att brytas ut mot etanolen så borde reflektionsvinkeln ≥ 90°.
n(glas) * sin c = n(etanol) * sin (90)
n(glas) = (n(etanol) * sin (90)) / sin (c)
n(glas) = (1,36 * 1) / sin (63,2) = 1,524
Nu har jag fått fram brytningsindex för glas och...där tar det stopp. Vad gör jag nu? Tänker jag rätt?
Tack på förhand!
Du får fram ett lägsta värde på prismats brytningsindex från villkoret att du måste ha totalreflexion från prisma till etanol med given infallsvinkel.
Vad blir infallsvinkeln mot den andra luftytan? Brytningsvinkeln är given och ger prismats index.
Okej. Eftersom ljuset totalreflekteras tillbaka ner i prismat även om reflektionsvinkeln är mer än 90° så blir n(glas) ≥ 1,524. Har jag fattat det rätt?
Infallsvinkeln som bryts ut mot den andra luftytan räknar jag ut så här:
Brytningsvinkeln borde vara 90° - b = 90° - 26,8° = 63,2°
n(glas) * sin (infallsvinkel) = n(luft) * sin(brytningsvinkel)
(infallsvinkel) = arcsin( (n(luft) * sin(brytningsvinkel)) / n(glas) ) = arcsin ( (1 * sin(63,2)) / 1,524) = 35,85...
Detta kan dock inte vara rätt eftersom infallsvinkeln enligt facit ska vara 36,4°. Är dessutom lite osäker på hur man vet om strålen lämnar prismat parallellt med gränsytan mot etanolen! I facit står det att det inte finns ett sådant värde, men jag förstår inte varför.
Röd vinkel: 63.2°
Grön vinkel: 90° - 63.2°= 26.8°
Orange vinkel: 180° - 2*26.8° = 126.4°
Från orange vinkel får du dra bort 90° för att få infallsvinkeln, som då blir 36.4°.
Den brutna vinkeln ut i luften skulle jag också ha gjort röd då den är 63.2°. Brytningslagen ger då
n*sin(36.4°) = 1*sin(63.2°)
så
n = sin(63.2°)/sin(36.4°) ≈ 1.504 < 1.524
De två kraven på totalreflexion och att strålen går ut parallellt med den reflekterande ytan går alltså inte att uppfylla samtidigt.
Dr. G skrev :...
De två kraven på totalreflexion och att strålen går ut parallellt med den reflekterande ytan går alltså inte att uppfylla samtidigt.
Tack snälla för den pedagogiska lösningen! Nu förstår jag hur jag ska tänka kring den här uppgiften.
