Svår uppgift integraler
Hej, har stött på följande uppgift:

Jag har försökt rita upp den men vet ej hur jag ska gå vidare.
Hur har du ritat?
Ja:
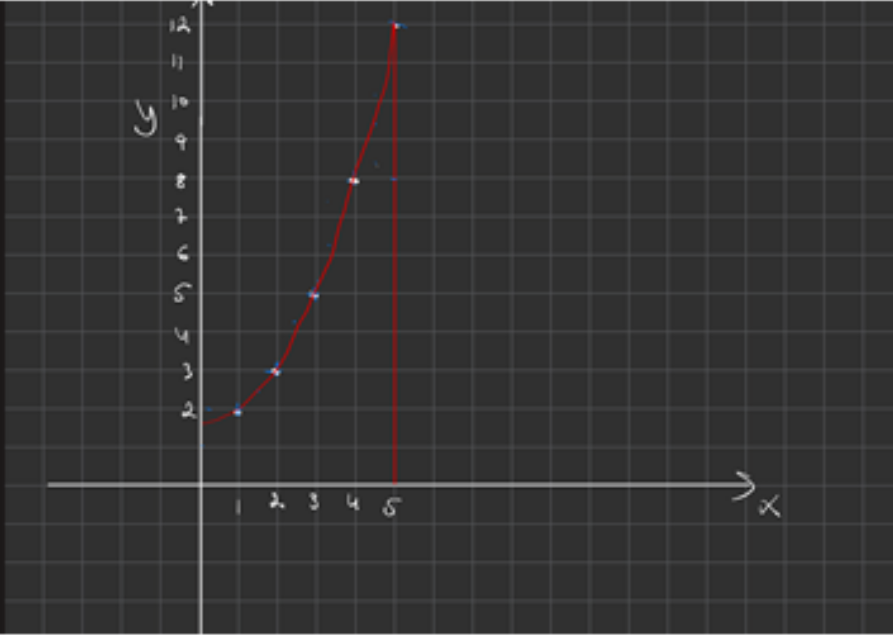
Lite suddigt kanske, men jag har försökt att dra en rak linje där x = 5 för att tydliggöra. Jag tänker att man på något sätt måste beräkna arean under.
Hur många hela rutor befinner sig under kurvan mellan x=1 och x=5?
Hur många icke-hela rutor befinner sig under (och därmed även över) kurvan mellan x=1 och x=5?
Icke hela rutor är 19 st. Hela rutor är 30 st. Har jag räknat rätt? Varför gjorde du så?
Anonym_15 skrev:Icke hela rutor är 19 st. Hela rutor är 30 st. Har jag räknat rätt? Varför gjorde du så?
Nej. Mellan x=1 till x=5. Du räknade från x=0 till x=5.
Varför jag gjorde så är för att ett sätt att få fram ett värde som är mindre än integralen är att göra en approximativ uträkning av arean under integralen. Att räkna antal hela rutor därunder är en approximativ lägre gräns av integralens värde.
Nu när jag räknar får jag att med icke - hela rutor är det 18 st och med hela rutor är det 28 st. Vad betyder det egentligen? Och hur vet du t.ex. att antalet icke - hela rutor ger den nedre gränsen och att hela rutor ger den övre gränsen? Förstår inte riktigt hur det går ihop
Hur fick du antalet hela rutor till 28?
Räknade så här:
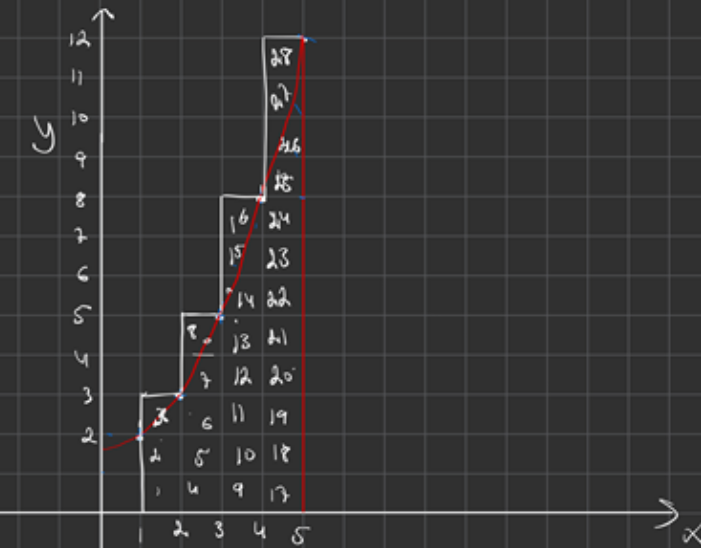
De rutor som genomskärs av kurvan är de som jag menade var icke-hela. Dvs. ruta nummer 3, 7, 8, 14, 15, 16, 25, 26, 27 och 28.
Så du menar att jag bara ska räkna icke hela rutorna för sig och sedan hela rutor för sig?
Det jag egentligen ville komma fram till är att vi vill approximera en undre gräns för integralen med antalet hela rutor under kurvan. Därför räknar vi antalet hela rutor under kurvan; deras yta är mindre än integralen, för vi får ju inte med bitarna som vi betecknat som icke-hela.
Vill vi sedan få en övre gräns får vi ta ett värde som definitivt är större än integralen får vi räkna de icke-hela rutorna som hela; då får vi ett värde som innefattar hela integralen och något mer.
Jaha, okej jag tror jag förstår. Så hur många icke - hela och hela rutor ska det då vara för att det ska bli rätt?
Räkna. I din bild i inlägg #9 har du redan räknat antal hela + antal icke-hela rutor.
Ja, 28 st.
Då har du ett värde större än integralen.
Hur många hela rutor är där?
18 st.
Då har du ett värde mindre än integralen.
Jämför detta med uppgiftsbeskrivningen.
Tack! Tror jag förstår lite bättre.


