Svår problemlösning gällande trigonometriska satserna
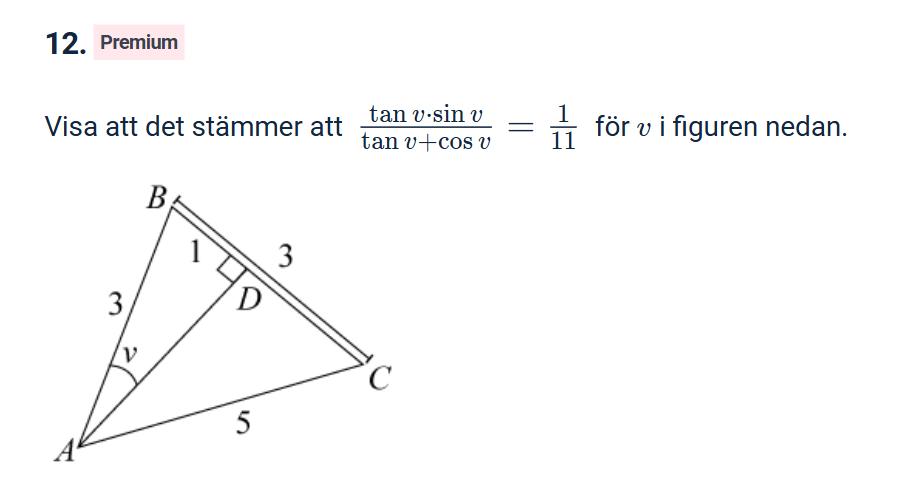
I denna fråga tänker jag följande:
Eftersom triangel ABD är rätvinklig måste även ADC vara rätvinklig för att deras vinklar tillsammans ska bli 180 grader. Eftersom BC är 3 cm och BD är 1 cm måste DC vara 2 cm. Mha. pythagoras sats kan AD beräknas:
AD =  = roten ur 21.
= roten ur 21.
Därefter beräknar jag sin v, cos, v och tan v för att sedan sätta in i uttrycket. Men jag får att uttrycket blir 1/24 och inte 1/11. Vad gör jag fel?
Denna uppgift är fel. Den där triangeln kan inte existera.
Från triangeln ABD kan vi också räkna ut AD med pythagoras och då får vi att
AD = √32-12=√8. Men √8≠√21
Men om vi ignorerar allt förutom triangeln ABD kan vi lösa den och få fram svaret som frågan ställer. Testa att bara kolla på ABD
Hur kan jag då, med hjälp av triangeln ADC bevisa att uttrycket stämmer?
Och hur kommer det sig att triangeln inte kan existera?
Anonym_15 skrev:Och hur kommer det sig att triangeln inte kan existera?
Vi kan få fram värdet på AD genom att kolla på den rätvinkliga triangeln ABD och då får vi fram att
AD =√8, eller så kan vi kolla på ADC som också är rätvinklig. Då får vi fram att AD =√21. Men AD kan inte ha två olika längder samtidigt
Men det enda man behöver för att lösa uppgiften är att kolla på ABD. Ta fram värdena på sinv, cosv och tanv utifrån ABD
Triangeln med sidorna 3,3,5 existerar men drar man linjen från A till D blir det antingen inte en rät vinkel vid D eller blir avståndet BD inte 1

