Svår fråga angeånde olikheter i trig-ekv
Hej!
Jag har en fråga om hur jag kan lösa följande uppgift utan grafiska miniräknare;
sin3x <0.5
och senare
sin(3x+40) < 0.5
Det ända jag kan ta fram är skärningspunkterna! Men det hjälper ju inte mig särskilt mycket!
Du kan börja med att lösa sin(x) < 0,5
Macilaci skrev:Du kan börja med att lösa sin(x) < 0,5
Jo, asså jag kom ju fram till skärningspunkterna med sin3x<0.5 och kommit fram till rätt intervall. Men för att lyckas lösa intervallen korrekt behöver jag rita upp grafen. Det är bara att om jag inte lyckas rita upp grafen rätt (ex pga att trig-ekv är för svår för att rita upp), så kan mina intervall bli helt fel.
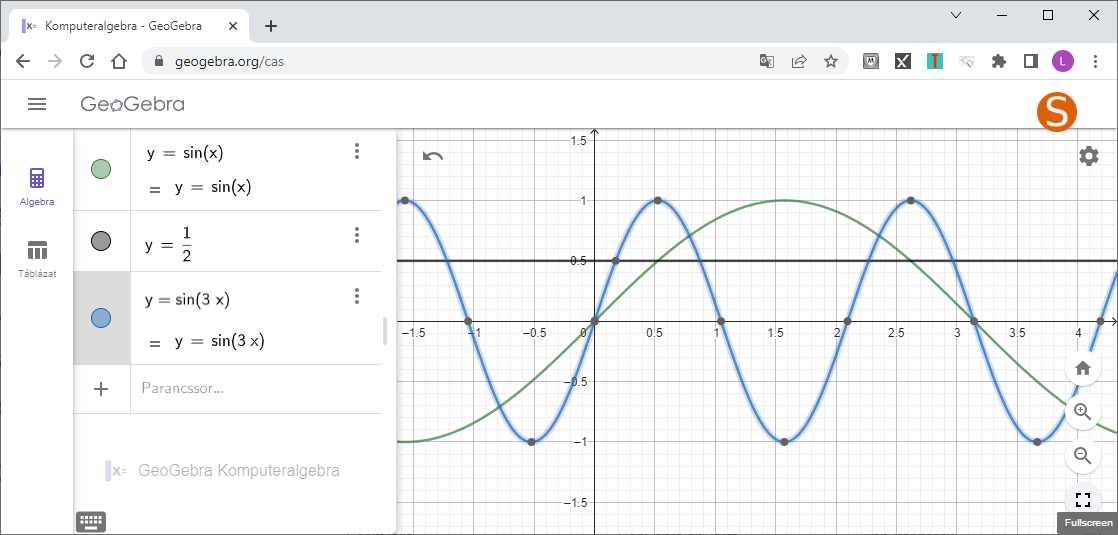
Du kan kontrollera dina resultat (din graf) med geogebra:
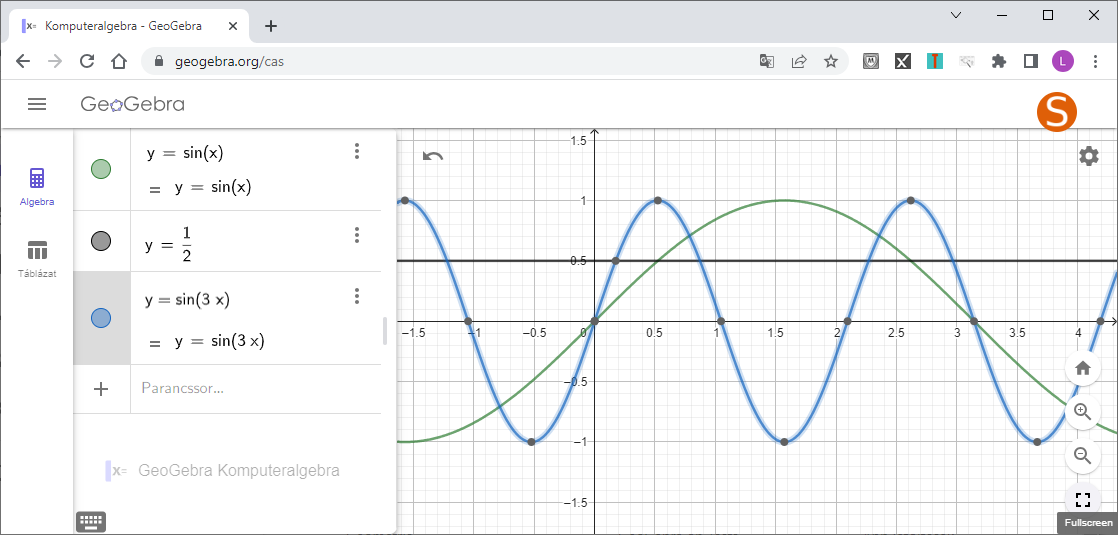
Macilaci skrev:Du kan kontrollera dina resultat (din graf) med geogebra:
Ja, det var det jag gjorde. Fast jag satte sin(3xdeg) så vi får det i grader. Men min fråga nu är hur jag kan lösa sin(3x+40) <0.5 algebraiskt, med tanke på att grafen förskjuts.
Anonym2005 skrev:Macilaci skrev:Du kan kontrollera dina resultat (din graf) med geogebra:
Ja, det var det jag gjorde. Fast jag satte sin(3xdeg) så vi får det i grader. Men min fråga nu är hur jag kan lösa sin(3x+40) <0.5 algebraiskt, med tanke på att grafen förskjuts.
säg i intervallet 0<x<180
Den algebraiska lösningen (med hjälp av grafen):
150o + n*360o < 3x + 40o < 390o + n*360o
110o + n*360o < 3x < 350o + n*360o
36.67o + k*120o < x < 116.67o + k*120o
---------
I 0o<x<180o intervallet:
36.67o < x < 116.67o och 156.67o < x < 180o
Macilaci skrev:Den algebraiska lösningen (med hjälp av grafen):
150o + n*360o < 3x + 40o < 390o + n*360o
110o + n*360o < 3x < 350o + n*360o
36.67o + k*120o < x < 116.67o + k*120o
---------
I 0o<x<180o intervallet:
36.67o < x < 116.67o och 156.67o < x < 180o
Hur kommer det sig att du gjorde "150o + n*360o < 3x <..."? Vad fick dig att skriva att ...<3x?
När jag vill lösa sin(x) < 0,5 försöker jag först hitta x värden där sin(x) = 0,5.
Och de är 30o, 150o, 390o, 510o,... osv.
Man kan skriva det som
150o + n*360o och 390o + n*360o
eller
30o + n*360o och 150o + n*360o
Intervallet där sin(x) är mindre än 0,5 är
150o + n*360o < x < 390o + n*360o
Och sedan gjorde jag inget annat, men skrev (3x + 40o) i stället för x.
Macilaci skrev:När jag vill lösa sin(x) < 0,5 försöker jag först hitta x värden där sin(x) = 0,5.
Och de är 30o, 150o, 390o, 510o,... osv.
Man kan skriva det som
150o + n*360o och 390o + n*360o
eller
30o + n*360o och 150o + n*360o
Intervallet där sin(x) är mindre än 0,5 är
150o + n*360o < x < 390o + n*360o
Och sedan gjorde jag inget annat, men skrev (3x + 40o) i stället för x.
Okej! Jag förstår. Men jag undrar bara hur du stället upp detta
"Intervallet där sin(x) är mindre än 0,5 är
150o + n*360o < x < 390o + n*360o"
Är det något man bara ska kunna, eller finns det någon man borde veta innan för att ställa upp det på det viset?
Man ska veta att
- sin(30o) = 0,5
- sinusfunktionen är periodisk med 360o period
- sinusfunktionen är symmetrisk kring x=90o (och x=270o)
Macilaci skrev:Man ska veta att
- sin(30o) = 0,5
- sinusfunktionen är periodisk med 360o period
- sinusfunktionen är symmetrisk kring x=90o (och x=270o)
Okej! Men hur hjälper det mig att förstå detta?
"Intervallet där sin(x) är mindre än 0,5 är
150o + n*360o < x < 390o + n*360o"
Jag skulle göra så här.
Sätt v = 3x. Olikheten blir då sin(v) < 0,5.
Rita en enhetscirkel och lägg in en horisontell linje på höjden 0,5.
Denna linje skär enhetscirkeln vid vinklarna v = 30° och v = -210°.
Markera den del av enhetscirkeln som ligger under den horisontella linjen.
Denna del av enhetscirkeln motsvarar olikheten sin(v) < 0,5.
Den markerade delen kan beskrivas som -210° < v < 30°.
Eftersom sinusfunktionen är periodisk så får vi alla lösningar genom att skriva -210°+n*360° < v < 30°+n*360°, där n är ett heltal.
Vi byter nu tillbaka från v till 3x vilket ger oss -210°+n*360° < 3x < 30°+n*360°.
Efter division av hela olikheten med 3 får vi
-70°+n*120° < x < 10°+n*120°.
Hängde du med?