Svår A uppgift
Hej, har stött på denna:
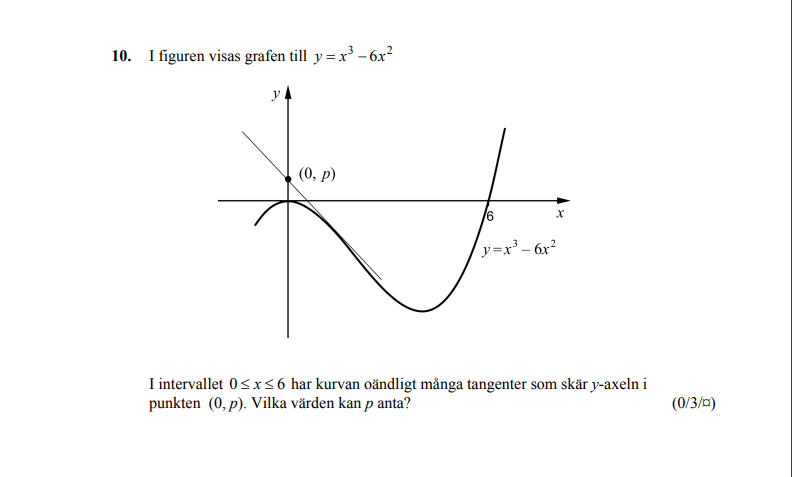
Hur skall jag börja?
Hej.
Jag tolkar uppgiftslydelsen som att det i intervallet finns oändligt många tangenter som skär y-axeln och att de efterfrågar vilka dessa skärningspunkter är.
En bra början är då att derivera funktionen.
Det kan vara värdefullt att ta reda på vilka möjliga värden denna derivata kan ha i intervallet.
Nästa steg kan vara att ta fram ett uttryck y = kx+m för tangenten, där både k och m beror på tangeringspunktens x-koordinat.
Här är inflextionspunkten x=2 viktig för det maximala p.
Den minimala p erhålles för punkten (6,0).
Precis, jag har börjat med att derivera funktionen och fick då: y =. Därefter försökte jag även skriva ett uttryck för tangentens k - värde. Dvs delta y/ delta x. Jag får då att k - värdet blir: x3- 6x2-p / x. Sedan hittade jag maximala och minimala lutningen som tangenten kan ha genom att lösa ut för y'(0) och y'(6). Jag satte tillslut upp en olikhet där tangentens k värde måste vara större eller lika med lutningen då x= 0 och mindre eller lika med lutningen då x=6. Jag får dock bara att p ska vara större eller mindre än tal med termer i x. Vad gör jag fel.
Tangentens k-värde är lika med derivatans värde I tangeringpunjten, inte delta y/delta x.
y'(0) ger inte vare sig den minimala eller maximala lutningen.
Rita deivatans graf så ser du det.
Jag förstår inte. Om jag ritar derivatans graf får jag ju en andragradsfunktion där ena nollstället är x=0.
Hur ska jag gå tillväga? p - värdet = m värdet för den räta linjen.
Derivatan ger tangentens lutning i en punkt, antag att x är för den punkten.
Funktionens värde för den punkten är
Tangenten måste gå genom punkten .
Anonym_15 skrev:Jag förstår inte. Om jag ritar derivatans graf får jag ju en andragradsfunktion där ena nollstället är x=0.
Ja, derivatans graf (se bild) visar att tangentens minsta k-värde fås vid x = 2 och att tangentens största k-värde fås vid x = 6.

Det minsta k-värdet är alltså y'(2) och det största k-värdet är y'(6).
Du ser även att tangenterna antar alla lutningar mellan dessa ytterligheter.
Kommer du vidare då?


