Svängningstiden pendel

 Jag förstå inte riktigt hur man gör när man lägger till vinkeln. vanligen brukar jag beräkna
Jag förstå inte riktigt hur man gör när man lägger till vinkeln. vanligen brukar jag beräkna
T med formeln: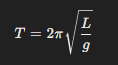 Det står ju att S=L*vinkeln men hur får man fram T från där?
Det står ju att S=L*vinkeln men hur får man fram T från där?
Edit: facit 2.15 sekunder
micke2z skrev:
Jag förstå inte riktigt hur man gör när man lägger till vinkeln. vanligen brukar jag beräkna
T med formeln:Det står ju att S=L*vinkeln men hur får man fram T från där?
Den formeln kan man bara använda när vinkeln är liten - då kan man anse att sin(v) är ungefär lika med 1 hela tiden, men i den här uppgiften gör pendeln så stora utslag att man måste ta hänsyn till att sin(v) varierar.
Smaragdalena skrev:micke2z skrev:
Jag förstå inte riktigt hur man gör när man lägger till vinkeln. vanligen brukar jag beräkna
T med formeln:Det står ju att S=L*vinkeln men hur får man fram T från där?
Den formeln kan man bara använda när vinkeln är liten - då kan man anse att sin(v) är ungefär lika med 1 hela tiden, men i den här uppgiften gör pendeln så stora utslag att man måste ta hänsyn till att sin(v) varierar.
Ja, jag de visste jag att vinkeln va för stor i detta fallet. Men jag tycker de beräknar de så konstigt för jag hittar inte någon liknande formel i formelsamlingen.
micke2z skrev:
jag hittar inte någon liknande formel i formelsamlingen.
Du ska nog använda informationen i grafen.
Jag lämnar denna uppgiften till ljussinniga att lösa, då jag ska se ifall min lärare kan förklara detta för mig.
Jag tycker det är bara konstigt att: om man använder vanliga pendel formeln vs facit så blir det inte stor skillnader på resultat. Och jag tänker de borde finnas ett enkelt sätt o göra detta på, möjligtvis grafiskt på miniräknaren. Hade jag försökt beräkna något sådant i verkligheten hade jag förstå vela få mer med info en bara längden på snöret och vinkeln. Och man tänker varför finns de inte riktigt en formel för högre vinklar när de finns till konisk pendelrörelse, och de finns säkert men då bör de hänvisa de i boken.
Jag vet mycket väl att en Kurva / radie = vinkeln -> som blir till vinkeln * radie = kurva som är hela sträckan bollen åker.
micke2z skrev:borde finnas ett enkelt sätt o göra detta på,
Jovisst, som jag skrev: använd Fig. 6.
Pieter Kuiper skrev:micke2z skrev:borde finnas ett enkelt sätt o göra detta på,
Jovisst, som jag skrev: använd Fig. 6.
Ja man kan läsa av den lite halvdant, men jag lustigt för jag kan ju inte ta upp grafen när jag har prov eller något annat. Det måste ju finnas ett bättre sätt o lösa en vanlig pendel.
micke2z skrev:
jag kan ju inte ta upp grafen när jag har prov
Det är inte ovanligt med provuppgifter där det finns information i form av en graf. Man ska kunna använda sådant.
Figur 6 är inte särskilt användbar - den visar pendelkulans höjd som funktion av tiden för vinklarna 89o och 30o, men inte för 60o som det är i uppgiften.
Smaragdalena skrev:Figur 6 är inte särskilt användbar - den visar pendelkulans höjd som funktion av tiden för vinklarna 89o och 30o, men inte för 60o som det är i uppgiften.
Jo, men då ligger rätt svar för 60o däremellan.
Inte vid medelvärdet, men jag tror att det är uppgiftens mening att göra en rimlig uppskattning utifrån Fig. 6. Alternativt fortsätter texten kanske på nästa sida, och då kan det finnas bättre information där.






