Surjektiva funktioner (diskret matematik)
Hej!
Har en uppgift där man ska bestämma hur många surjektiva funktioner f : {1, 2, . . . , 8} → {1, 2, . . . , 7} existerar.
Detta är svaret. Det står att den första delen kommer från att man ska välja två element som har samma funktionsvärde. Hur vet man att det är just två som ska väljas? Och kommer 8 från att det är 1...8 element i första mängden?
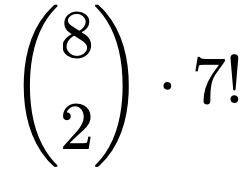
För en surjektiv funktion är värdemängden = målmängden, dvs alla värden i målmängden måste antas för något värde i definitionsmängden.
Från detta inses att precis 2 element från definitionsmängden måste peka på samma element i målmängden, medan de andra 6 pekar på unika element.
Hade fler element uppfyllt detta hade funktionen ej varit surjektiv.
Uppenbarligen kan inte färre element uppfylla detta.


