Summa av en Serie (2)

$\sum _{n=0}^{\infty }\frac{1}{e^n}=\sum _{n=0}^{\infty }\frac{1^n}{e^n}=\sum _{n=0}^{\infty }{\left(\frac{1}{e}\right)}^n$

$$\begin{gathered} a=1 \\ r =\hspace{0.17em}\frac{1}{e} \end{gathered}$$

$\frac{a}{1-r}=\frac{1}{1-{\displaystyle \frac{1}{e}}}=e·\frac{1}{1-{\displaystyle \frac{1}{e}}}=\frac{e}{e-1}$

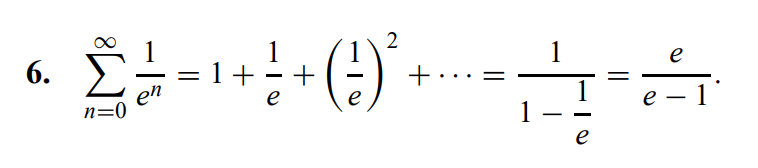
beerger skrev:

$\sum _{n=0}^{\infty }\frac{1}{e^n}=\sum _{n=0}^{\infty }\frac{1^n}{e^n}=\sum _{n=0}^{\infty }{\left(\frac{1}{e}\right)}^n$

$$\begin{gathered} a=1 \\ r =\hspace{0.17em}\frac{1}{e} \end{gathered}$$

$\frac{a}{1-r}=\frac{1}{1-{\displaystyle \frac{1}{e}}}=e·\frac{1}{1-{\displaystyle \frac{1}{e}}}=\frac{e}{e-1}$

Jag är helt med på det. Ok. Men borde inte den geometriska serien vara skriven i formen $\displaystyle ar^{n-1}$??????

$$\begin{gathered} \frac{1}{e}·{\left(\frac{1}{e}\right)}^{n-1} då n =\hspace{0.17em}0 är \\ \frac{1}{e}·{\left(\frac{1}{e}\right)}^{0-1} =\hspace{0.17em}\frac{1}{e}·{\left(\frac{1}{e}\right)}^{-1}=\frac{1}{e}·\left(\frac{1}{{\displaystyle \frac{1}{e}}}\right)=\frac{e}{e}=1 \end{gathered}$$

Nej, det är inget krav! I dina böcker så börjar serien ofta på n = 1.

$\sum _{n=1}^{\infty }a{r}^{n-1}=\sum _{n=0}^{\infty }a{r}^n$

Tänk på att a i $\frac{a}{1-r}$ är första elementen i serien oavsett vilket n den börjar ifrån. T.ex. i

$\sum _{n=5}^{\infty }{\left(\frac{1}{b}\right)}^n$

så är $a={\left(\frac{1}{b}\right)}^5$

beerger skrev:

Tänk på att a i $\frac{a}{1-r}$ är första elementen i serien oavsett vilket n den börjar ifrån. T.ex. i

$\sum _{n=5}^{\infty }{\left(\frac{1}{b}\right)}^n$

så är $a={\left(\frac{1}{b}\right)}^5$

Okok! Fick nu en tydligare bild än hur boken beskriver det i alla fall! Tack så mycket:)