Statistik - Sufficient statistics, vad är nyttan av den?

Såg detta i samband med följande exempel:

Låt $p(X=1|\mu) = \mu$ och $p(X=0|\mu)=1-\mu$, där $0 \leq \mu \leq 1$ , då kan X distribution beskrivas med bernoulli och med MLE av log likelihood ger (2.7)

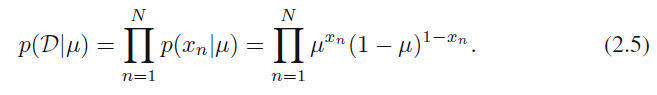
Då kallas $\sum_{n=1}^{N} x_{n}$ i (2.6) för sufficient statistic för datan över distributionen eller något i stil med detta, eftersom enligt boken så beror log likelihood funktionen på N observationer x_n endast genom deras summa $\sum_{n=1}^{N} x_{n}$.

Det jag inte fattar är vad är nyttan med detta? I vilket fall kommer jag behöva använda datan för att utföra MLE i syfte att ta reda på $\mu$, så det är inte så att datan förenklas eller försvinner eller något, bara att jag kanske abstraherar bort från att behöva tänka på att direkt behöva jobba med datan, då jag har någon sorts funktion som jag kan stoppa in data i och så får jag tillbaka något värdefullt som jag kan använda för log likelihood funktionen.
Min poäng är att jag hade fortfarande kunnat utföra MLE helt eller någon annan punktskattning eller annan estimeringsmetod för $\mu$ om jag bara arbetade på vanligt sätt och inte tänkte på sufficient statistics.