sudd kast - enkel (Fysik/Fysik 2)

Eftersom du kommer att behöva använda rörelseekvationerna vid konstant acceleration ofta så är det lika bra att vänja sig vid dem.

De fungerar i alla sammanhang där det är likformigt föränderlig rörelse, dvs konstant acceleration. Exempelvis vid kaströrelser/fritt fall utan friktion/luftmotstånd, som i ditt exempel med suddet.

===== Gör då så här =====

Inför ett koordinatsystem med horisontell x-axel så att suddet rör sig i positiv x-riktning och en vertikal y-axel pekandes uppåt.

Lägg origo vid markplan precis under utkastpositionen.

Då gäller följande för suddets position (x, y) som funktion av tiden:

x(t) = x₀+v_0xt+a_xt²/2

y(t) = y₀+v_0yt+a_yt²/2

Samt följande för suddets hastighetkomposanter (v_x, v_y) som funktion av tiden:

v_x(t) = v_0x+a_xt

v_y(t) = v_0y+a_yt

Där

x₀ = startposition I x-led [m]
y₀ = startposition I y-led [m]
v_0x = starthastighet i x-led [m/s]
v_0y = starthastighet i y-led [m/s]
a_x = acceleration i x-led [m/s²]
a_y = acceleration i y-led [m/s²]
t = tiden [s]

Alla startpositioner, starthastigheter och accelerationen är kända eller kan beräknas, förutom y₀, eftersom det inte framgår från vilken höjd suddet kastas.

Tips:

När suddet når sin högstanhöjd är v_y(t) = 0.
När suddet når marken är y(t) = 0

Tackar enormt för det du skrivit och tipsen.

Om vi börjar med a) frågan, hur långt suddet kommer,

Då vill vi ha ett läge, alltså är y(t) lämplig här? Jag är inte inne i tankesättet än men jag tror att man ska räkna fram hur lång tid det tar tills den landar för att sedan kunna räkna ut sträckan? Men huruvida jag ska avgöra vad som behövs för att räknas ut i y-led och x-led känner jag mig osäker på.

naturnatur1 skrev:

Om vi börjar med a) frågan, hur långt suddet kommer,

Då vill vi ha ett läge, alltså är y(t) lämplig här?

Ja, om du har lagt koordinatsystemet så att x-axeln ligger i markhöjd så är suddets y-koordinat lika med 0 då det är i markhöjd.

Alltså får du då ut tidpunkten för landning genom att lösa ekvationen y(t) = 0.

Kalla denna tidpunkt t₁

Jag är inte inne i tankesättet än men jag tror att man ska räkna fram hur lång tid det tar tills den landar för att sedan kunna räkna ut sträckan?

Det stämmer. Med hjälp av ovanstående så vet du att suddet landar vid t = t₁.

Om du då har lagt koordinatsystemet så att x = 0 vid utkastpunkten så får du fram kastlängden genom att beräkna x(t₁).

Men huruvida jag ska avgöra vad som behövs för att räknas ut i y-led och x-led känner jag mig osäker på.

Jag förstår inte riktigt vad du menar här. Kan du förtydliga?

Hur vet jag vilken formel jag ska använda vid beräkning av tiden?

Det jag menade var att jag inte riktigt förstår hur jag ska avgöra när man ska räkna fram hastigheten i x-led, y-led eller kombinera dessa.

naturnatur1 skrev:
Hur vet jag vilken formel jag ska använda vid beräkning av tiden?

Du vet y-positionen när suddet landar. Då kan du använda formeln för y(t) för att beräkna tidpunkten t₁ då suddet landar.

Det jag menade var att jag inte riktigt förstår hur jag ska avgöra när man ska räkna fram hastigheten i x-led, y-led eller kombinera dessa.

Du vet att v_y = 0 då suddet når sin högsta punkt (eftersom det vänder där och börjar falla neråt igen).

Då kan du använda formeln för v_y(t) för att beräkna tidpunkten då suddet når sin högsta punkt. Kalla denna tidpunkt t₀.

Då får du höjden genom att beräkna y(t₀).

===== Sammanfattning =====

Ekvationen y(t) = 0 ger dig tidpunkten då suddet landar.
Ekvationen v_y(t) = 0 ger dig tidpunkten då suddet når sin högsta höjd.

y(t) = y₀ + v_0y + at²/2

0 = ? + 12 + (-9,82)t² / 2

Varför använder man inte denna formel

y = v₀ x sin(x) x (t) - gt²/2

Tillägg: 11 okt 2023 12:52

Ursäkta om jag blandar ihop tal och formler nu. Men jag har lite svårt nu till en början att avgöra vilken formel som är lämplig vid kaströrelse samt vilka värden som ska sättas in.

Det är samma formel

Men det är v₀ som är lika med 12 m/s, inte v_0y.

Rita en bild över hastigheten v₀0i utkastögonblicket.

v_0x och v_0y är x- och y-komposanterna av denna ursprungshastighet.

Detär där sinud och cosinusbför vinkeln kommer in.

Yngve skrev:
Det är samma formel

Men det är v₀ som är lika med 12 m/s, inte v_0y.

Rita en bild över hastigheten v₀0i utkastögonblicket.

v_0x och v_0y är x- och y-komposanterna av denna ursprungshastighet.

Hur är de samma? Den ena är för konstant accelererad rörelse medan den andra är för sneda kast,där vinkeln är inkluderad.

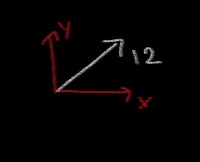
Menar du såhär?

Tillägg: 11 okt 2023 12:58

Ser nu att du syftat på enbart på hastigheten i y-led och satt in i starthastigheten i y-led i "konstant acceleration" formeln, om jag förstått rätt?

Vad blir y₀ i detta fallet? 0?

naturnatur1 skrev:

Hur är de samma? Den ena är för konstant accelererad rörelse medan den andra är för sneda kast,där vinkeln är inkluderad.

De formler jag gav är generella formler som fungerar i alla sammanhang där det handlar om likformigt föränderlig rörelse, dvs konstant acceleration.

Menar du såhär?

Ja, om vi dessutom anger vinkeln så ser vi att v_0x = v₀•cos(25°) och att v_0y = v₀•sin(25°):

Tillägg: 11 okt 2023 12:58

Ser nu att du syftat på enbart på hastigheten i y-led och satt in i starthastigheten i y-led i "konstant acceleration" formeln, om jag förstått rätt

Som sagt, de formler jag angav är generella.

naturnatur1 skrev:
Vad blir y₀ i detta fallet? 0?

Det framgår inte av uppgiften från vilken höjd suddet kastas, så det går inte att säga med säkerhet vad y₀ är.

Detta gör även att det inte går att lösa a-uppgiften enbart med den information som är given.

Men om vi antar att y₀ t.ex. har värdet 1,5 meter (eller 0 meter) så går det utmärkt att lösa även a-uppgiften.

Okej, då börjar jag med att räkna ut tiden när suddet slås ner på marken.

0 = 0 + 12 + (-9,82)t² /2

9,82t²/2 = 12

9,82t² = 24

t = roten ur 24/9,82 som cirka är

1,56 s.

Hur långt den når, kan jag beräkna detta genom

s = v₀ x cos(x) multiplicerat med tiden

men det blir fel svar?

Upptäckte felet!

Jag har med resultant hastigheten, när jag endast ska ha med den i y-led.

$v_{0} \times \sin α \times t - g t^{2} / 2 = s t r ä c k a i y - l e d 12 \times \sin 25 \times t - (9, 82) t^{2} / 2 = 0 5, 04 t = - 9, 82 t^{2} / 2 10, 14 t = 9, 82 t^{2} 10, 14 = 9, 82 t t = 10, 14 / 9, 82 = c a 1, 03 s$

sedan lägger jag in det i

v₀ x cos(25) x 1,03 och det fås till ca 11m, vilket stämmer.

B frågan

Hur högt över utgångshöjden kommer suddet?

Vad menas med detta? Menar de högsta punkten?

Om ja, så satte jag in den i

y_max = v² x sin(2x)² / 2g

och får svaret till 4,3.

Facit svarar 6m?

naturnatur1 skrev:
B frågan

Hur högt över utgångshöjden kommer suddet?

Vad menas med detta? Menar de högsta punkten?

När de skriver "hur högt över utgångshöjden" så menar de y_max-y₀

Om ja, så satte jag in den i

y_max = v² x sin(2x)² / 2g

och får svaret till 4,3.

Facit svarar 6m?

Det är svårt att förstå vad du skriver när du använder symbolen x på två andra sätt än att avse en x-koordinat:

Vinkeln (som du istället borde kalla v)
Multiplikationssymbol (du borde istället använda • eller *)

Men din formel stämmer inte och svaret I facit stämmer inte heller.

Formeln bör vara $y_{diff}=\frac{{v_0}^2\cdot\sin^2(v)}{2g}$ , vilket blir ungefär 1,3 meter.

Kan du ladda upp en bild på facit?

Uppgiften ska egentligen lösas grafiskt, men jag vill kunna lösa det algebraiskt.

Jag har tyvärr inte lösningsförslaget. Uppgiften är från en powerpoint genomgång från min lärare, här är facit:

I svaret står det "maxhöjd" men i uppgiften står det "höjd över utgångshöjden". Det är bara samma sak om ursprungshöjden är 0.

Kan du även ladda upp en bild på uppgiften?

OK då var det en dåligt formulerad uppgift eftersom det inte står från vilken höjd suddet kastas.

Men vi kan anta att y₀ = 0, dvs att suddet kastas från marknivå (hur det nu ska gå till).

Detta eftersom kastlängden då blir just cirka 11 meter.

Svaret på b-uppgiften ör som sagt fel.

Försök nu att lösa c-,uppgiften på egen hand med hjälp av de formler jag skrev i svar #2.

Yngve skrev:
OK då var det en dåligt formulerad uppgift eftersom det inte står från vilken höjd suddet kastas.

Men vi kan anta att y₀ = 0, dvs att suddet kastas från marknivå (hur det nu ska gå till).

Detta eftersom kadtlängden då blir just cirka 11 meter.

Svaret på b-uppgiften ör som sagt fel.

Försök nu att lösa c-,uppgiften på egen hand med hjälp av de formler jag skrev i svar #2.

I x-led använder jag

$L ä g e : v_{0} \times \cos α \times t 12 \times \cos (25) \times 2 \approx 21, 75 m$

Y -led:

$L ä g e : v_{0} \times \sin α \times t - (g t^{2} / 2) L ä g e : 12 \times \sin (25) \times 2 - (9, 82 \times 2^{2} / 2)$

Som cirka blev -9,5 , vilket är helt orimligt?

Ja, båda svaren är orimliga.

Ser du varför och vad felet är?

Den bildar en parabel väl? Den når sitt högsta läge vid ca 1,03s alltså bör det ta 2,06s tills den landar?

Antigen är det något med det eller räknefel eller något med gravitationen (tecken)

Ja, det är en parabel.

Men det stämmer inte att den når sin högsta punkt efter cirka 1,03 sekunder. Hur kommer du fram till det?

Yngve skrev:
Nja, inte riktigt.

Varför tror du att den når sin högsta punkt efter cirka 1,03 sekunder?

För att den kraften vi gav vid utkastet kommer att "tas ut" av gravitationen. Sedan kommer den vända och istället accelerera nedåt (när den vertikala dominerar, om man får uttrycka det så)

Tillägg: 12 okt 2023 00:52

Oj, jag blandade ihop det med a frågan..

Tillägg: 12 okt 2023 00:54

Jag hade i åtanke att det var tiden det tog för att nå sitt högsta läge. Men det är inte alls så, fel av mig!

Ja, den vertikala hastigheten kommer att minska på vägen upp, nå värdet 0 vid högsta punkten och sedan bli negativ under suddets färd neråt.

Men hur kommer du fram till att den når sin högsta punkt då t $\approx$ 1,03 s?

Yngve skrev:
Ja, den vertikala hastigheten kommer att minska på vägen upp, nå värdet 0 vid högsta punkten och sedan bli negativ under suddets färd neråt.

Men hur kommer du fram till att den når sin högsta punkt då t $\approx$ 1,03 s?

Jag blandade ihop det med fråga a =D Vilket är fel, men tänkte det var tiden den nådde sin max höjd..

OK. Men vad händer egentligen vid t $\approx$ 1,03 s?

Den når 11 m horisontellt.

Ja, och den landar då även på marken.

Kastet pågår alltså bara i cirka 1,03 sekunder.

Så att fråga om var suddet befinner sig vid t = 2 sekunder är inte relevant.

Men om marken inte hade funnits där så skulle suddet ha fortsatt framåt och neråt även efter t = 1,03 s.

Och det skulle då ha befunnit sig vid den position som du beräknade i svar #21.

Uppgiften är alltså felfornulerad på flera sätt.

Yngve skrev:
Ja, och den landar då även på marken.

Kastet pågår alltså bara i cirka 1,03 sekunder.

Så att fråga om var suddet befinner sig vid t = 2 sekunder är inte relevant.

Men om marken inte hade funnits där så skulle suddet ha fortsatt framåt och neråt även efter t = 1,03 s.

Och det skulle då ha befunnit sig vid den position som du beräknade i svar #21.

Uppgiften är alltså felfornulerad på flera sätt.

Tack för hjälpen!

Tänk dig att du står högst upp i ett högt torn och kastar suddet.

Då är frågeställningen var det befinner sig efter 2,0 s relevant.