Strikt växande funktion, lös olikhet

När en funktion är strängt växande betyder det (lite informellt) att funktionens värde ökar när $x$ ökar. 
Ett exempel på en strängt växande funktion är $e^x$. Ju större $x$ blir, desto större blir $e^x$. Men för många funktioner stämmer detta inte. Ett exempel är $x^3-x$. För $x=0$ blir funktionens värde 0, men om vi sätter in typ $x = \frac 12$ får vi $\frac 18 - \frac 12 = -\frac 38$. 

Tänk då om du har just olikheten $0 < \frac 12$. Detta är en sann olikhet. Om vi låter $f(x) = e^x$ och, som i definitionen som du bifogade, tar $f$ på båda sidor får vi $f(0) < f(\frac 21)$, alltså $e^0 < e^{\frac 12}$. Detta är också sant, $e^{\frac 12} \approx 1.64$.
Men om vi istället låter $f(x) = x^3-x$ får vi inte en sann olikhet när vi tar $f$ på båda sidor.

Vi kan säga att en strängt växande funktion behåller dessa olikheter eftersom det alltid stämmer att ett större värde på $x$ ger ett större värde på funktionen. Men för funktioner som är avtagande någonstans stämmer inte detta, som vi såg i exemplet med $x^3-x$. Även om $x=\frac 12$ är ett större värde än $x=0$ är inte funktionens värde det eftersom att funktionen är avtagande just där. 

PS: Vill också nämna att funktioner kan vara växande eller avtagande under vissa intervall. För exemplet $x^3-x$ är den avtagande när $0\leq x < \frac{1}{\sqrt{3}}$ (egentligen lite längre bak). När x är större än $\frac{1}{\sqrt{3}}$ är den också strängt växande.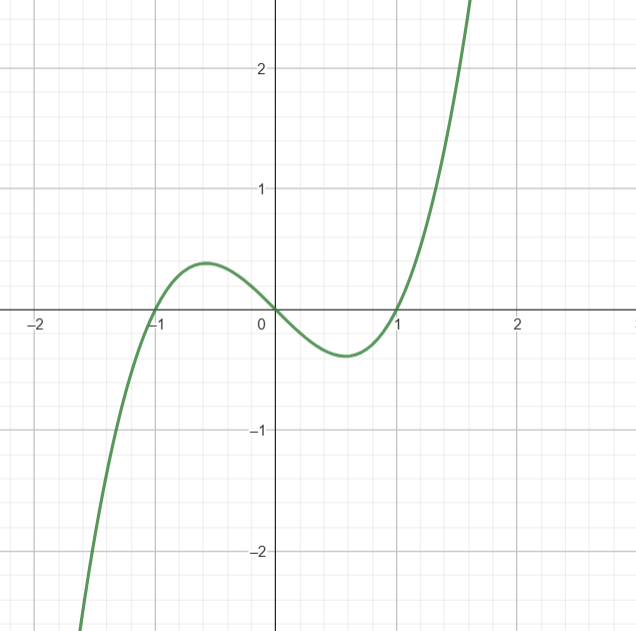
Såhär ser funktionen ut. 

Ja, strikt och strängt växande är samma sak. Rent logiskt är det det kontrapositiva påståendet som används i detta exempel.

Nu tror jag att jag har fattat vad som menas med strängt växande. Med strängt växande funktion så menar man att om man har ett intervall (a,b)  samt att funktionen är definerad i alla x i intervallet (a,b) så är funktionen strängt växande om x1 < x2 (från intervallet) samt f(x1) < f(x2). 

Men jag fattar liksom inte resonemanget att "Eftersom ln är strikt växande funktion är det ekvivalent med x^2 + x - 6 ≤ x" Vad menar facit ens? Facit har ju gett en förklaring till varför man kan ta bort ln uttrycken från VL samt HL men jag fattar inte det resonemanget 

samma resonemang används även på denna uppgift:

Facit menar följande: Låt $f(x)$ vara en strikt växade funktion och antag att $f(a)\leq f(b)$. Då måste $a\leq b$.

Bevis: Antag motsatsen, att $a>b$. Eftersom $f(x)$ är strikt växande, så måste enligt definitionen $f(a)>f(b)$. Detta är en motsägelse. Alltså måste $a\leq b$.

Om vi låter $f(x)=\ln(x)$, $a=x^2+x-6$ och $b=x$, så får vi situationen i första lösningsförslaget.

Gustor skrev:

Facit menar följande: Låt $f(x)$ vara en strikt växade funktion och antag att $f(a)\leq f(b)$. Då måste $a\leq b$.

Bevis: Antag motsatsen, att $a>b$. Eftersom $f(x)$ är strikt växande, så måste enligt definitionen $f(a)>f(b)$. Detta är en motsägelse. Alltså måste $a\leq b$.

Om vi låter $f(x)=\ln(x)$, $a=x^2+x-6$ och $b=x$, så får vi situationen i första lösningsförslaget.

Asså jag fattar inte helt ärligt.... När jag tittar på definitionen så kopplar jag den inte alls till uppgifterna... jag förstår inte alls :( 

Om ln(A) är mindre än ln(B), så måste A vara mindre än B.

Kör bil i uppförsbacke: Om bil A är lägre än bil B, så måste bil A ha kört kortare än bil B.

Bubo skrev:

Om ln(A) är mindre än ln(B), så måste A vara mindre än B.

Kör bil i uppförsbacke: Om bil A är lägre än bil B, så måste bil A ha kört kortare än bil B.

Det är jag såklart med på... att ju större tal inuti parentesen i ln så ger det större svar för då måste exponenten i e vara större... men vad har det med uppgiften att göra? 

I din uppgift är A.   x^2 + x - 6 

I din uppgift är B.  x

Bubo skrev:

I din uppgift är A.   x^2 + x - 6 

I din uppgift är B.  x

Asså jag fattar inte hur detta förklarar att man kan ta bort ln uttrycket... 

brunbjörn skrev:

Gustor skrev:

Facit menar följande: Låt $f(x)$ vara en strikt växade funktion och antag att $f(a)\leq f(b)$. Då måste $a\leq b$.

Bevis: Antag motsatsen, att $a>b$. Eftersom $f(x)$ är strikt växande, så måste enligt definitionen $f(a)>f(b)$. Detta är en motsägelse. Alltså måste $a\leq b$.

Om vi låter $f(x)=\ln(x)$, $a=x^2+x-6$ och $b=x$, så får vi situationen i första lösningsförslaget.

Asså jag fattar inte helt ärligt.... När jag tittar på definitionen så kopplar jag den inte alls till uppgifterna... jag förstår inte alls :( 

Om vi har den gamla olikheten $\ln{(x^2+x-6)} \leq \ln x$
Vi vet att både $\ln x$ och $e^x$ är strängt växande. Om vi då låter $f(x) = e^x$ får vi från definitionen att $f(\ln{(x^2+x-6)}) \leq f(\ln{x})$ stämmer. Alltså $e^{\ln{(x^2+x-6)}} \leq e^{\ln{x}}$
Då tar $e$ och $\ln$ ut varandra och vi får 
$x^2 + x -6 \leq x$

AlexMu skrev:

brunbjörn skrev:

Visa föregående citat

Gustor skrev:

Facit menar följande: Låt $f(x)$ vara en strikt växade funktion och antag att $f(a)\leq f(b)$. Då måste $a\leq b$.

Bevis: Antag motsatsen, att $a>b$. Eftersom $f(x)$ är strikt växande, så måste enligt definitionen $f(a)>f(b)$. Detta är en motsägelse. Alltså måste $a\leq b$.

Om vi låter $f(x)=\ln(x)$, $a=x^2+x-6$ och $b=x$, så får vi situationen i första lösningsförslaget.

Asså jag fattar inte helt ärligt.... När jag tittar på definitionen så kopplar jag den inte alls till uppgifterna... jag förstår inte alls :( 

Om vi har den gamla olikheten $\ln{(x^2+x-6)} \leq \ln x$
Vi vet att både $\ln x$ och $e^x$ är strängt växande. Om vi då låter $f(x) = e^x$ får vi från definitionen att $f(\ln{(x^2+x-6)}) \leq f(\ln{x})$ stämmer. Alltså $e^{\ln{(x^2+x-6)}} \leq e^{\ln{x}}$
Då tar $e$ och $\ln$ ut varandra och vi får 
$x^2 + x -6 \leq x$

Fast varför säger du just att f(x) = e^x  ? dvs vad har det med ln(x² + x -6)  ≤ ln(x) att göra ? Dessutom fattar jag inte varför jag bara inte direkt kan ta bort ln uttrycken utan att motivera att ln(x) är strängt växande... (jag fattar att ln(x) är strängt växande  i intervallet (0,∞) men varför ens nämna det.... )

brunbjörn skrev:

AlexMu skrev:

Visa föregående citat

brunbjörn skrev:

Gustor skrev:

Facit menar följande: Låt $f(x)$ vara en strikt växade funktion och antag att $f(a)\leq f(b)$. Då måste $a\leq b$.

Bevis: Antag motsatsen, att $a>b$. Eftersom $f(x)$ är strikt växande, så måste enligt definitionen $f(a)>f(b)$. Detta är en motsägelse. Alltså måste $a\leq b$.

Om vi låter $f(x)=\ln(x)$, $a=x^2+x-6$ och $b=x$, så får vi situationen i första lösningsförslaget.

Asså jag fattar inte helt ärligt.... När jag tittar på definitionen så kopplar jag den inte alls till uppgifterna... jag förstår inte alls :( 

Om vi har den gamla olikheten $\ln{(x^2+x-6)} \leq \ln x$
Vi vet att både $\ln x$ och $e^x$ är strängt växande. Om vi då låter $f(x) = e^x$ får vi från definitionen att $f(\ln{(x^2+x-6)}) \leq f(\ln{x})$ stämmer. Alltså $e^{\ln{(x^2+x-6)}} \leq e^{\ln{x}}$
Då tar $e$ och $\ln$ ut varandra och vi får 
$x^2 + x -6 \leq x$

Fast varför säger du just att f(x) = e^x  ? dvs vad har det med ln(x² + x -6)  ≤ ln(x) att göra ? Dessutom fattar jag inte varför jag bara inte direkt kan ta bort ln uttrycken utan att motivera att ln(x) är strängt växande... (jag fattar att ln(x) är strängt växande  i intervallet (0,∞) men varför ens nämna det.... )

ln är motsatsen (inversen) till $e^x$ när du "direkt tar bort" ln uttrycken är det du egentligen gör att höja båda sidor upp med $e$. $e$ och ln tar ut varandra. Vi måste motivera att $\ln{x}$ är strängt växande eftersom att, som du ser på reglerna där uppe, om den inte var det så kanske inte olikheten skulle stämma när ln uttryckten tas bort. (I mitt fall använde jag $e^x$, så jag skulle behövt motivera att $e^x$ var strängt växande men det är samma princip)

brunbjörn skrev:

Nu tror jag att jag har fattat vad som menas med strängt växande. Med strängt växande funktion så menar man att om man har ett intervall (a,b)  samt att funktionen är definerad i alla x i intervallet (a,b) så är funktionen strängt växande om x1 < x2 (från intervallet) samt f(x1) < f(x2). 

Men jag fattar liksom inte resonemanget att "Eftersom ln är strikt växande funktion är det ekvivalent med x^2 + x - 6 ≤ x" Vad menar facit ens? Facit har ju gett en förklaring till varför man kan ta bort ln uttrycken från VL samt HL men jag fattar inte det resonemanget 

samma resonemang används även på denna uppgift:

 

Jag förstår uppgiften jag har citerat nu. Förklaringen är att när vi har: ln( (2x+1)(x-1)²) = ln(11x-5) så kan vi ta bort ln uttrycken eftersom ln(x) , x > 0 är injektiv. Om en funktion är injektiv så innebär det per definition att (2x+1)(x-1)² = (11x-5). Definionen är att om f(x) är injektiv så gäller f(x1) = f(x2) så måste x1=x2. Om f(x) = ln(x) så kan vi alltså skriva ln( (2x+1)(x-1)²) = ln(11x-5) som (2x+1)(x-1)² = (11x-5).

Men uppgiften jag skrev ett inlägg om innehåller en olikhet... Jag hade kunnat använda mig utav defintionen av injetivitet om det endast stod ln(x² + x -6)  =  ln(x) men nu är det ju inte så... Kan jag använda mig utav defintionen av injektivitet OCH defintionen för strängt växande för att förklara varför man kan ta bort ln tecknet? ln(x), x > 0 är ju en injektiv funktion och en strängt växande funktion...  

fast är inte ln(x) , x >0 även växande? Kan jag inte använda det som argument för att ta bort ln uttycket istället för att använda argmentet att den är strängt växande? Anledningen till att jag inte vill använda argumenetet att den är strängt växande är för att defintionen för strängt växande använder sig inte av lika med tecknet... Hur tänkte facit.... defintionen för strängt växande använder ju sig endast av < och inte lika med tecknet.....