Sträckan AP

Hur stor är vägskillnaden, AP-BP , i punkten P?

Kan du förutom ovanstående samband med vägskillnaden, se något annat (geometriskt) samband mellan AP och BP som du kan utnyttja?

Hur beräknar jag vägskillnaden AP-BP? Är punkten P andra ljudminimum?

Q kan jag beräkna, men jag vet inte om detta hjälper mig?

Pythagoras sats?

Hur resonerade du för att komma fram till att Q var första min? 

Borde du inte kunna använda samma typ av resonemang för att komma fram tilll vilket min punkten P är?

Pythagoras låter bra!

Hur resonerade du för att komma fram till att Q var första min? 

"I punkten Q finner man för första gången ett ljudminimum" - utifrån den meningen

Borde du inte kunna använda samma typ av resonemang för att komma fram tilll vilket min punkten P är?

Det kan man säkert, men hur? (: De ligger dock på samma linje men det är väl fortfarande olika våglängder?

Våglängden är konstant - du vet ju att frekvensen är 1,7 kHz.

Ja, det står i uppgiften att det är _en_ ton. Det står också i uppgiften att man närmar sig högtalare B längs den streckade linjen (från långt håll). När man är på jättelångt håll så är vägskillnaden nästan noll. När du kommer till Q så har vägskillnaden vuxit till 0.5*lambda. När du kommer till P så har vägskillnaden vuxit till...

När du kommer till P så har vägskillnaden vuxit till...

1,5λ?

1,5 x 0,2 = 0,3m

Så 0,3 är vägskillnaden, dvs AP - BP 

Ja, precis! Förstår du varför?

Jag förstår beräkningen. Men jag förstår dock inte hur man kunde anta att den var 1,5λ?

Och eftersom jag har vägskillnaden, AP-AB, och jag vill ha AP, men hur får jag reda på den? Jag har en katet som är 0,6m, men sedan har jag varken AP eller BP? (endast skillnaden mellan dessa längder)

Tänk dig den rätvinkliga triangeln som utgörs av punkten A, punkten B, och dig själv. Antag att du är jätte-jätte-jättelångt ifrån punkten B. Då är triangels vinkel i "din punkt" jätte-jätte-jättespetsig, dvs hypotenusan och den långa kateten är i stort sett lika långa, du befinner dig i stort sett i centralmax.

Om du sedan börjar gå mot B, så kommer den spetsiga vinkeln i triangeln att bli succesivt trubbigare, och löngdskillnaden mellan kateterna kommer att öka, så först kommer du till en punkt där vägskillnaden är 0.5*lambda (första min). Sedan kommer du till en punkt där vägskillnaden är 1*lambda (första max), sedan kommer du till en punkt där vägskillnaden är 1.5*lambda (andra min), etc etc. Fortsätter du att gå hela vägen till punkten B, så kommer vägskillnaden att växa till 0.6m.

Alltså, under hela din vandring till B kommer vägskillnaden succesivt att öka från 0m till 0.6m på ett strängt växande sätt. Dvs du kommer att stöta på _alla_ max och min som finns i interferensmönstret. 

Hänger du med?

Ja typ. Är sträckan AP alltså 0,3m? Men är inte det en vägskillnad?

Tänk dig den rätvinkliga triangeln som utgörs av punkten A, punkten B, och dig själv. Antag att du är jätte-jätte-jättelångt ifrån punkten B. Då är triangels vinkel i "din punkt" jätte-jätte-jättespetsig, dvs hypotenusan och den långa kateten är i stort sett lika långa, du befinner dig i stort sett i centralmax.

Om du sedan börjar gå mot B, så kommer den spetsiga vinkeln i triangeln att bli succesivt trubbigare, och löngdskillnaden mellan kateterna kommer att öka, så först kommer du till en punkt där vägskillnaden är 0.5*lambda (första min). Sedan kommer du till en punkt där vägskillnaden är 1*lambda (första max), sedan kommer du till en punkt där vägskillnaden är 1.5*lambda (andra min), etc etc. Fortsätter du att gå hela vägen till punkten B, så kommer vägskillnaden att växa till 0.6m.

Är med på detta.

Fortsätter du att gå hela vägen till punkten B, så kommer vägskillnaden att växa till 0.6m.

Men om jag går ner hela vägen till punkten B så kommer det väl vara som att sträcka AP - 0? Eller är jag ute och cyklar nu?

Edit: just det. 0,6 - 0..

Är sträckan AP alltså 0,3m? Men är inte det en vägskillnad?

Hur kom du fram till detta? Kan du förklara?

 just det. 0,6 - 0..

Ja! Nu förstår du, eller hur?

Det sista förstår jag. Men jag förstår inte hur jag ska ta reda på sträckan AP.

Först bestämdes våglängden (0,2m) #1

Därefter vet vi att det i punkten Q är första ljudminimum, och sedan att punkten P var andra ljudminimum (vilket jag inte riktigt förstår hur man antog det, för att vara ärlig). (Eller var det bara en tolkningsgrej/läsförståelse i frågan?) 

Så för att beräkna vägskillnaden ----- 1,5λ (λ  = 0,2) så 1,5 x 0,2 = 0,3m

Men dessa 0,3m beskriver en vägskillnad, alltså AP-BP. Vi är endast ute efter AP. Genom pythagoras sats kan man säkert lösa ut AP (men man har endast en katet given - 0,6m). Jag förstår inte hur man får fram AP?

Ekv1 (vägskillnad):

AP-BP=0.3

Ekv2(Pythagoras):

AP^2-BP^2=0.6^2

Jag förstår tyvärr inte riktigt.

Förlåt! Jag hade lite ont om tid och inte möjlighet att formattera. Du har som du säger, två okända sidor AP och BP i den rätvinkliga triangeln. Men du har också två villkor som ska uppfyllas: 

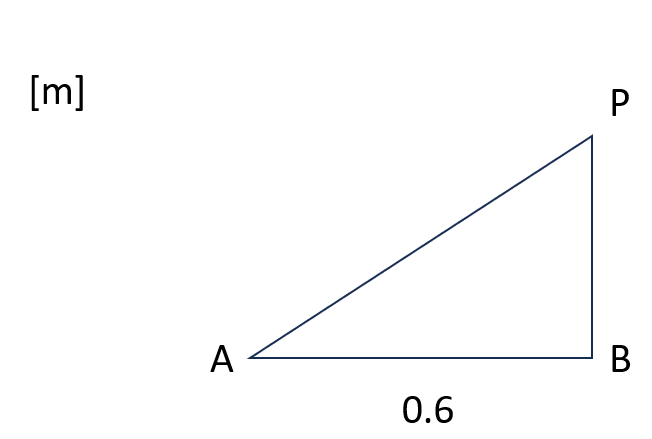
Villkoret för vägskillnaden ger: AP-BP=0.3

Villkoret för rätvinklig triangel ger: BP² + 0.6² =AP²

Hänger du med?

No worries. Ja det gör jag!

Tillägg: 16 jan 2024 19:25

Ekvationssystem?

Ja, precis!

AP är 0,75m. Kan det stämma?

naturnatur1 skrev:

AP är 0,75m. Kan det stämma?

Ja det tror jag stämmer. Räkna ut BP också, för att bli ännu mer övertygad om att det stämmer.

BP blev 0,45.

Tillägg: 16 jan 2024 19:35

Med kontroll får jag att AP blev 0,75

Ja. 0.75-0.45=0.3

Det verkar stämma, eller hur?

Ah okej. Här kunde vi alltså räkna ut den sträckan mha ett ekvationssystem. Vi hade våglängden och sedan kombinerade vi det med pythagoras! Snyggt. Tack för hjälpen!

JohanF skrev:

Tänk dig den rätvinkliga triangeln som utgörs av punkten A, punkten B, och dig själv. Antag att du är jätte-jätte-jättelångt ifrån punkten B. Då är triangels vinkel i "din punkt" jätte-jätte-jättespetsig, dvs hypotenusan och den långa kateten är i stort sett lika långa, du befinner dig i stort sett i centralmax.

Om du sedan börjar gå mot B, så kommer den spetsiga vinkeln i triangeln att bli succesivt trubbigare, och löngdskillnaden mellan kateterna kommer att öka, så först kommer du till en punkt där vägskillnaden är 0.5*lambda (första min). Sedan kommer du till en punkt där vägskillnaden är 1*lambda (första max), sedan kommer du till en punkt där vägskillnaden är 1.5*lambda (andra min), etc etc. Fortsätter du att gå hela vägen till punkten B, så kommer vägskillnaden att växa till 0.6m.

Alltså, under hela din vandring till B kommer vägskillnaden succesivt att öka från 0m till 0.6m på ett strängt växande sätt. Dvs du kommer att stöta på _alla_ max och min som finns i interferensmönstret. 

 

Hänger du med?

Angående detta. Om du befinner dig väldigt långt ifrån punkten B, till exempel vid punkten X i figuren, så kommer 

AX ≈ BX, dvs vägskillnaden blir AX-BX ≈ 0

Om du befinner dig vid punkten B så är vägskillnaden 0.6m (som du kom fram till igår). Alltså måste du när du färdas hela vägen från X till B, passera ställen där vägskillnaden är alla tal mellan 0 och 0.6. Dvs du kommer att träffa på alla nodlinjer som förekommer i interferensmönstret.

Ja just det, tack!