Största värde för integral
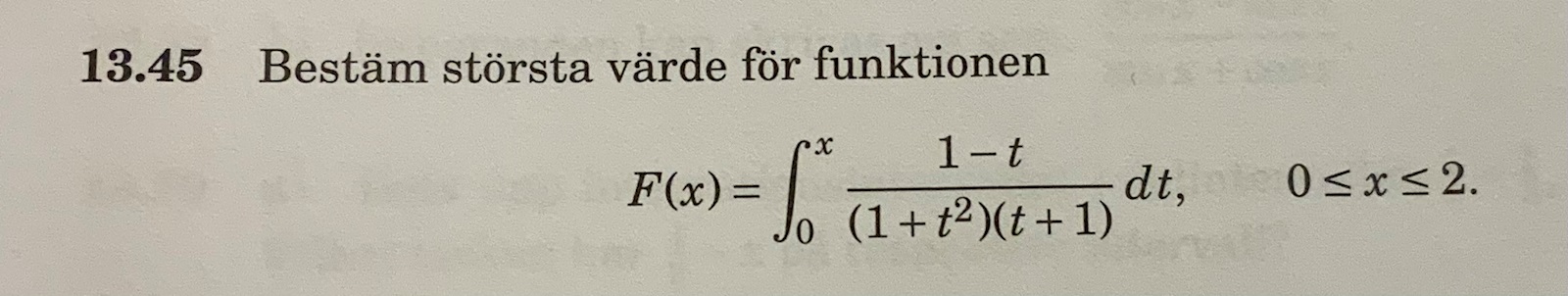
Hej, undrar hur jag ska gå till väga för att beräkna största värdet på denna integral. Har fått fram den primitiva funktionen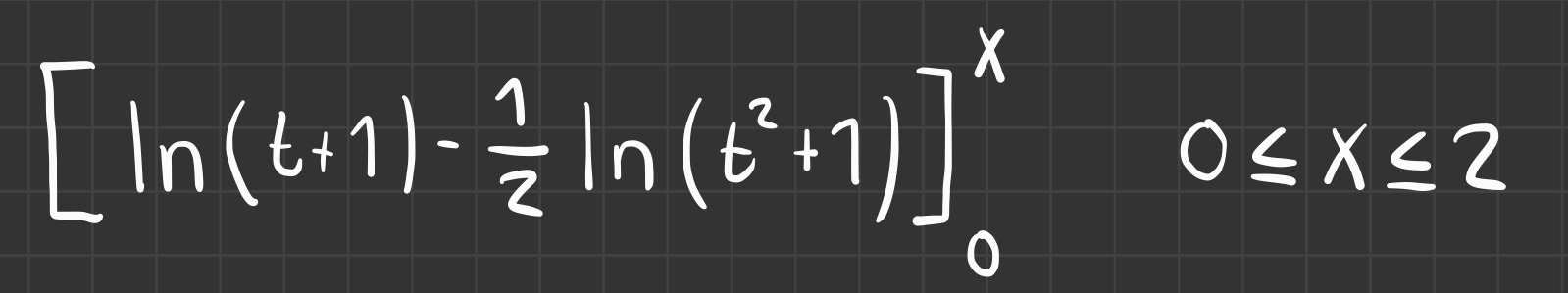 , och när jag sätter in x=1 blir funktionsvärdet 12ln2 vilket också är rätt svar enlight facit ( F(1) = 12ln2)
, och när jag sätter in x=1 blir funktionsvärdet 12ln2 vilket också är rätt svar enlight facit ( F(1) = 12ln2)
Men hur vet man att detta är största värde till denna funktion?
Tack på förhand
funktionen har ett nollställe vid t = 1. men eftersom f(t) > 0 om 0≤t≤1 så fås den största arean då vi går från 0 till 1 eftersom kurvan för t > 1 gör att f(t) < 0.
Tillägg: 15 jul 2022 19:23
Det borde stå f(t)≥0.
Är jag på rätt spår om jag resonerar som så att P(t) = 1-t(t^2+1)(t+1) när t = 1
Grafen P(t) är då positiv mellan och "samlar på sig" positiv area under grafen.
Men när t > 1 så blir grafen P(t) negativ och "samlar på sig" negativ area, vilket minskar värdet för F(x)?
Därför är arean som störst när t = 1
Precis. Men notera att arean är maximal när , då är Men jag är ganska säker på att du förstod det och att det var precis det du menade. Men bara så du inte förvirrar dig själv med vad som är och vad som är .
Men ja, jag hade resonerat likadant som du ser i mitt tidigare inlägg. :)


