Största resp minsta värde
Hej, vid beräkning av intervallsgränser tar man alltid hänsyn till extrempunkter?
Extrempunkter är väl alltid globala punkter, dvs de största/minsta värdena?
Jag förstår inte frågan. När beräknar man intervallgränser? Har du ett exempel?
Och vad är en global punkt?
Marilyn skrev:Jag förstår inte frågan. När beräknar man intervallgränser? Har du ett exempel?
Och vad är en global punkt?
Vi har funktionen y=2x^3-24x+8, vilka är de största/minsta funktionsvärdena inom intervallgränsen -3≤x≤-5? Analysera mha derivata och ta hänsyn till extrempunkter
Global punkt är väl största/minsta maximi och minimipunkten?
Marilyn skrev:Jag förstår inte frågan. När beräknar man intervallgränser? Har du ett exempel?
Och vad är en global punkt?

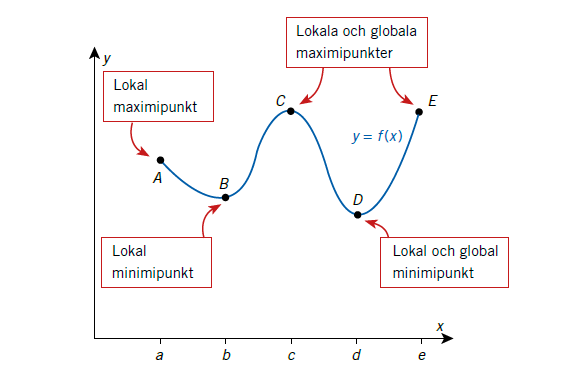
"Global punkt" betyder ingenting. Det handlar om lokala och globala extrempunkter/minimipunkter/maximipunkter.
Global betyder typ ”hela världen”.
En lokal maxpunkt kan vara en liten kulle på tomten, nerförsbacke i alla riktningar. En global maxpunkt är Chomolugma (Mount Everest) högsta berget på jorden.
När du söker en funktions lokala extrempunkter, så är den vanliga proceduren att derivera och göra teckenstudium i derivatans nollställen. Dessutom får man undersöka om ändpunkterna är max- eller min.
Om du söker största och minsta värde är det enklare. Du tar reda på kandidaterna och ser vilket x som ger störst respektive minst värde.
Om en funktion har max (eller min) så är det
–i en punkt där derivatan är noll
eller
– i en punkt där derivatan inte är definierad (t ex en spets på kurvan)
eller
– I en ändpunkt på kurvan.
Så det är bara att ta reda på dessa kandidater och sätta in motsvarande x-värden. Störst är globalt max, minst är globalt min.
Vi har också luriga fall där en funktion saknar ett största och/eller ett minsta värde.
Exempel:
f(x) = 2x3-3x2 saknar både största och minsta värde i intervallet -2 < x < 1.
Bra exempel! Även g(x) = x saknar största och minsta värde på a < x < b men din f(x) har både lokalt max och lok min i intervallet och saknar likafullt globala extrempunkter.
Tack till alla! Grym förklaring Marilyn, fattade inte riktigt vad global punkt innebar :D



