största och minsta värde (ej derivata)
1, Ange största och minsta värde av funktionen
f(x) = 3sin(x) - 4cos(x) + 1
Mitt svar: Eftersom sinx och cosx inte kan anta samma värde samtidigt tänkte jag att sinx kunde vara +1 och cosx kan vara -1. Då får man det största värdet tänkte jag, som är 8. Varför kan man inte tänka så?
Enligt facit är största värdet 6 och minsta -4. De skrev om funktionen till en sinus funktion. Jag förstår att man kan göra så men inte varför mitt sätt är fel.
naturarecheck skrev:1, Ange största och minsta värde av funktionen
f(x) = 3sin(x) - 4cos(x) + 1
Mitt svar: Eftersom sinx och cosx inte kan anta samma värde samtidigt tänkte jag att sinx kunde vara +1 och cosx kan vara -1. Då får man det största värdet tänkte jag, som är 8. Varför kan man inte tänka så?
Om du hade fått svaret 7 hade jag förstått hur du har tänkt, men hur fick du 8?
Enligt facit är största värdet 6 och minsta -4. De skrev om funktionen till en sinus funktion. Jag förstår att man kan göra så men inte varför mitt sätt är fel.
Som vanligt - rita! Här ser du hur kurvan 3 sin(x) och kurvan -4 cos(x) samverkar.
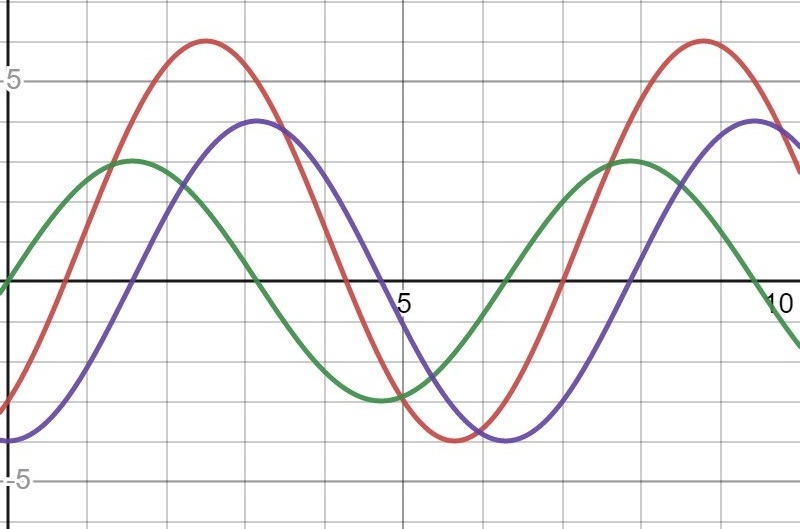
sinx och cosx kan faktiskt anta samma värde, nämligen för x = pi/4.
Men sinx kan inte vara 1 samtidigt som cosx är -1.
Jag fick 8 genom 3 + 4 + 1. Alltså 3 * 1 + (-4) * (-1) + 1. Fick jag fel för att jag glömde parantes? Skulle jag göra minus ettan?
naturarecheck skrev:Jag fick 8 genom 3 + 4 + 1. Alltså 3 * 1 + (-4) * (-1) + 1. Fick jag fel för att jag glömde parantes? Skulle jag göra minus ettan?
Nej, det var jag som hade tappat bort ettan. Nu är jag med på hur du tänkte.
Vet du varför jag fick fel svar? Ska det aldrig vara parantes där?
Du får fel svar eftersom du felaktigt antar att sin(x) kan vara 1 samtidigt som cos(x) kan vara -1.
Med samtidigt menar jag för ett och samma värde på x.
Det du kan göra för att lösa uppgiften är att skriva om 3sin(x) - 4cos(x) till något som ser ut som
A*sin(x-c), det finns en identitet för det
värdet på c behöver du inte bestämma eftersom man bara frågar efter största värdet, inte när det inträffar.
Tack Ture! Jag förstår nu :)




