Största area triangel integral.
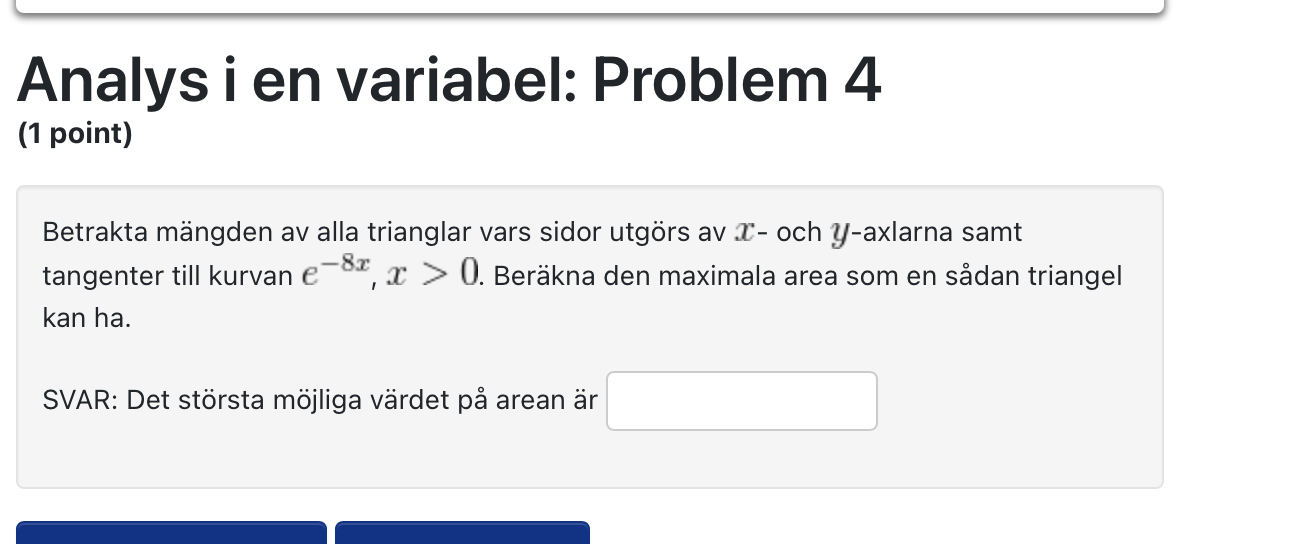
Hej, Jag har försökt att lösa denna uppgift. Men inte lyckats lösa den. Nedan på bilden har jag försökt att komma fram till lösningen.
Jag har skissat en bild och kommit fram till hur triangeln bör se ut. Tar punkten för x=0 har jag kommit fram till. Därefter försöker jag att komma fram till den andra slutpunkten. Jag tänker mig om jag lyckas teckna en funktion för den tangenter som ger stört area kan jag därefter sätta y=0 och få ut x-värdet.
Om jag får fram funktionen för aren tänker jag att jag kan derivera och ta fram maxvärden.
Och därefter integralerna funktionen.
Hur kan jag få fram funktionen? 
Jag skulle börja med att ta fram tangentens ekvation i en tangeringspunkt a.
För x= a är y = e-8a
tangentens lutning får vi med derivatans värde för x = a
k = -8e-8a
TAngentens ekvation får jag sen med enpunktsformeln
y-y1 = k(x-x1) sätt in dina värden på k och tangeringspunktens koordinater.
Sen borde det vara lätt att beräkna var tangenten skär axlarna, dvs där x = 0 resp y = 0 (som givetvis kommer att innehålla a)
om jag tänkt rätt borde du därefter kunna beräkna triangelns area och derivera map a.
Ture skrev:
Jag skulle börja med att ta fram tangentens ekvation i en tangeringspunkt a.
För x= a är y = e-8a
tangentens lutning får vi med derivatans värde för x = a
k = -8e-8a
TAngentens ekvation får jag sen med enpunktsformeln
y-y1 = k(x-x1) sätt in dina värden på k och tangeringspunktens koordinater.
Sen borde det vara lätt att beräkna var tangenten skär axlarna, dvs där x = 0 resp y = 0 (som givetvis kommer att innehålla a)
om jag tänkt rätt borde du därefter kunna beräkna triangelns area och derivera map a.
Tack Ture! Jag försökt att köra på ditt sätt men när jag gör det så lyckas jag inte att lösa uppgiften. Jag tror att detta beror på att jag faktiskt inte vet en faktiskt punkt utan att båda punkterna är uttrycka i a. Vilket leder till att jag får 0=0.
Jag testa att använda de punkterna som jag räknade där tangenter skär x-axeln (x-värdet, 0) och satta x-värdet=B (basen).
Och passa samma sätt i den andra punkter så får jag H (höjden) uttryckt i y-värdet. Sätter A(a)=(BH)/2 räknar fram maximum, och sätter in i A(a). Vilket ger rätt svar, jag tyckte först att det vara lika konstigt men jag resonerade sedan fram ett det verkar rimligt eftersom det jag har gjort är att med samma funktion skriva om dem på två olika sätta beroende av a. Därför tänker jag mig att eftersom att det är beroende av a så kommer den ena att ändras om den ändra att ändras. Tänker jag rätt?
Lösningar här nedan:
Kanske pratar vi förbi varandra, men det ser ut som om du gjort som jag menade.

Efter att ha skapat ett uttryck för tangentens ekvation, givet att den går genom a,f(a), så har jag beräknat punkterna A och B enligt figuren och får triangelns area
A*B/2 = 2ab+b/8 +8a2b
derivatan av b map a blir -8*e-8x = -8b, så om vi deriverar uttrycket för arean får jag
(2b+2a(-8b))-b+8(2ab+a2(-8)b) som vi sätter = 0 och förenklar till
2-16a-1+16a-64a2 = 0 som ger att a =1/8 (den negativa roten förkastar vi)
Arean orkar jag inte räkna ut...


