Störst och minsta värde
Bestäm största och minsta värdet i intervallet 1<x<3 ( det ska vara streck under dessa <, alltså kan x vara=1 och 3)
för funktionen f(x)=x^2-x+1.
Vet inte riktigt hur jag ska börja för att kunna lösa denna uppgift. Jag tänkte att jag skulle börja med att titta på dess extremvärden och hitta funktionens nollställen. Tänkte då att jag kunde använda pq-formeln men då blir det minus under roten ur vilket blir konstigt. Andra alternativet var att derivera funktionen ( vilket blir 2x-1) men vet inte hur jag ska gå vidare efter det?
Tacksam för hjälp:)
Största och minsta värde kan vara antingen där derivatan är 0, eller i intervallets ändpunkter om de ingår (somi det här fallet).
När jag deriverat så får jag f´(x)=2x-1 och sedan sätter jag detta till noll: 2x-1=0 men det är här som jag inte vet riktigt hur jag ska gå vidare. Får bara till att x=1/2 men borde väl vara två nollställen?
När jag fått fram extremvärdet så antar jag att jag ska jämföra funktionsvärdena för att se vilket det största samt minsta värdet är. Men vet inte hur jag gå vidare från början.
soeder99 skrev:När jag deriverat så får jag f´(x)=2x-1 och sedan sätter jag detta till noll: 2x-1=0 men det är här som jag inte vet riktigt hur jag ska gå vidare. Får bara till att x=1/2 men borde väl vara två nollställen?
Nej, varför det?
När jag fått fram extremvärdet så antar jag att jag ska jämföra funktionsvärdena för att se vilket det största samt minsta värdet är. Men vet inte hur jag gå vidare från början.
Räkna ut f(1) och f(3), du behöver inte beräkna f(½) eftersom det ligger utanför definitionsmängden.
Verkar som att 1/2 är fel när jag slår in funktionen i miniräknaren..
När jag räknar f(1) samt f(3) får jag ut att f(1)=1 och f(3)=7. Hur jag vidare då?
Rita.
När jag ritar grafen så ser det ut som att ekvationen saknar reella lösningar, alltså att att den har två komplexa rötter. Hur räknar jag då ut det största och minsta värdet?
Du skall inte ta fram största och minsta värdet, bara största och minsta värdet i intervallet.
Så det räcker med att jag vet f(1)=1 och att f(3)=7 när jag sätter in i funktionen? Att dessa är det största och minsta värdet i intervallet för funktionen?
soeder99 skrev:Så det räcker med att jag vet f(1)=1 och att f(3)=7 när jag sätter in i funktionen? Att dessa är det största och minsta värdet i intervallet för funktionen?
Rita funktionens graf i det aktuella intervallet.
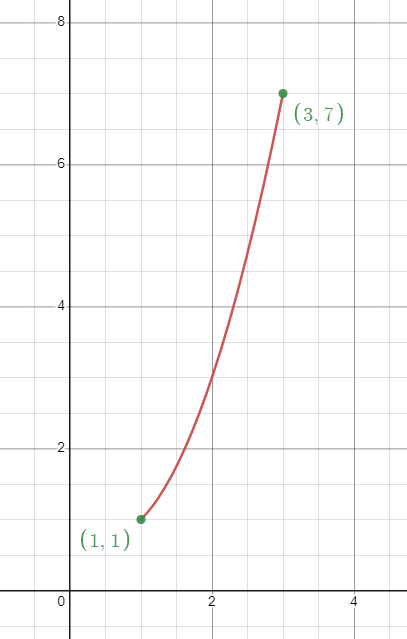
Då ser det ut som i bilden nedan, där du ser att
- det minsta värdet fås vid intervallets vänstra ändpunkt, dvs då x = 1. Detta minsta värde år 1.
- det största värdet fås vid intervallets högra ändpunkt, dvs då x = 3. Detta största värde är 7.