stjärngrafer
Skulle behöva lite hjälp med a)
Jag kom fram till att nästa (6,3 ) blir en stjärna med 2 sammanhängande komponenter, men kan man säga att den är sammanhängande om den har 2 sammanhängande komponenter? och hur får man (6,4) och (6,5)?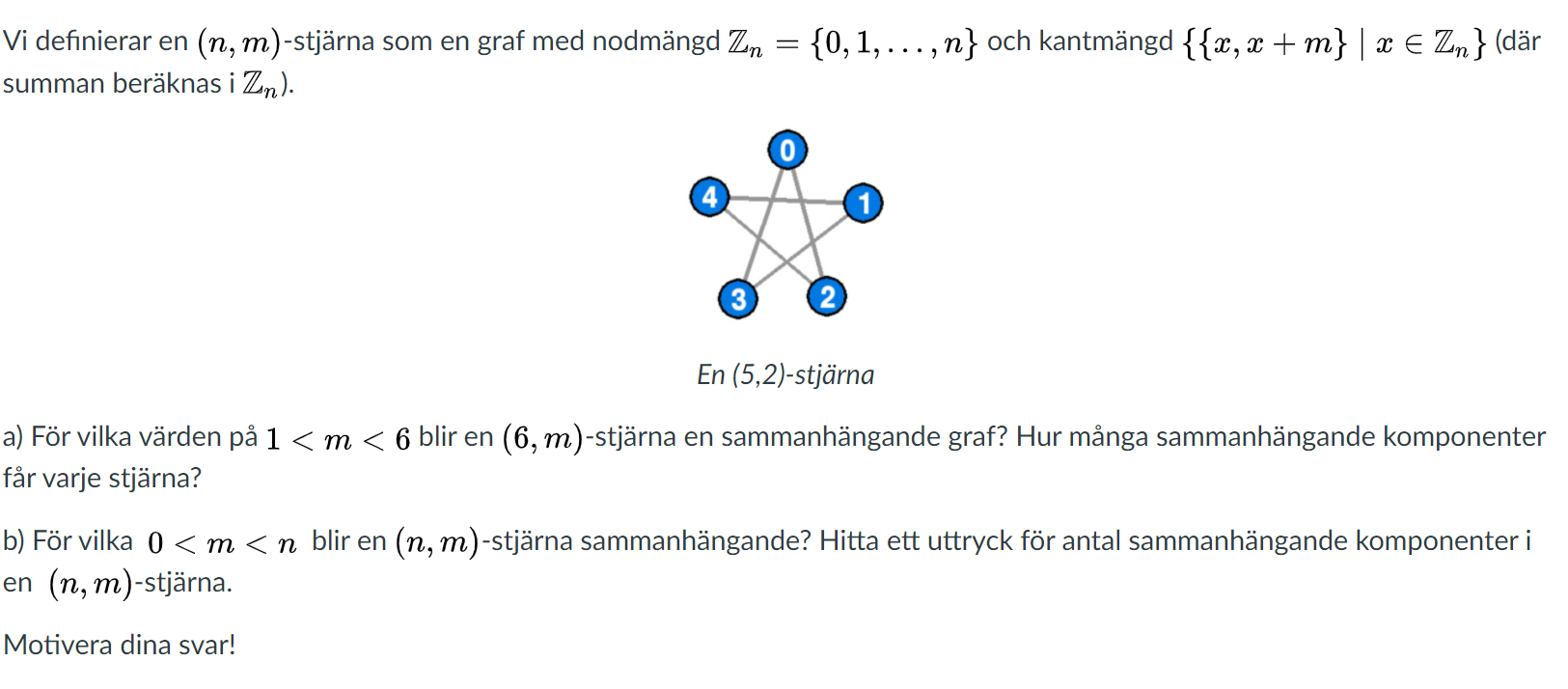
En graf som har två komponenter är inte sammanhängade. En graf är sammanhängande om den har exakt en komponent.
Det bör inte vara svårare att konstruera (6,4) och (6,5) än (6,2) och (6,3). Det är väl bara att rita.
ok! men visst borde det stämma att 6,2 inte är sammanhängande graf, medan resten är det med en sammanhängande komponent för 6,3, 6,4, och 6,5?
Men för övrigt tror jag inte att det stämmer att (6,3) har två komponenter, den bör ha 3. Vore bra att se vad du ritat.
Smutsmunnen skrev:Men för övrigt tror jag inte att det stämmer att (6,3) har två komponenter, den bör ha 3. Vore bra att se vad du ritat.
såg att jag skrev fel menade 6,2. :)
men hur hade du löst b uppgiften?
Nej (6,2), (6,3),(6,4) som uppgift a gäller så ska ingen vara sammanhängande.
(6,5) är däremot sammanhängande liksom (6,1) men uppgift a handlar ju inte om dem, däremot kanske du börjar se ett mönster inför b-uppgiften.
Förövrigt är problemet lite skevt formulerat. Av definitionen följer att nodmängden innehåller n+1 element, så grafen skulle innehålla n+1 noder, men av exemplet så tycks det röra sig om n noder. Vi ska nog förstå Z_n som innehållande 0 till n-1.
sven999 skrev:Smutsmunnen skrev:Men för övrigt tror jag inte att det stämmer att (6,3) har två komponenter, den bör ha 3. Vore bra att se vad du ritat.
såg att jag skrev fel menade 6,2. :)
men hur hade du löst b uppgiften?
Om du löser 6a) bör du få en ganska tydlig hypotes inför 6b.
Sedan hur man bevisar den kan vi ta när du formulerat hypotesen.
Vad är det för kurs förresten? Vilken termin matte? Första, andra?
nice! ska testa lite! Det är diskret matte första terminen
 har jag tänkt rätt här?
har jag tänkt rätt här?
Nej (6,3) har du fått fel,
I (6,3)
Det går en kant från 0 till 0+3=3 och från 3 en till 3+3=0
en kant från 1 till 1+3=4 och en från 4 till 4+3=1.
en kant från 2 till 2+3=5 och en från 5 till 5+3=2.
Grafen innehåller alltså bara 3 kanter.
Smutsmunnen skrev:Nej (6,3) har du fått fel,
I (6,3)
Det går en kant från 0 till 0+3=3 och från 3 en till 3+3=0
en kant från 1 till 1+3=4 och en från 4 till 4+3=1.
en kant från 2 till 2+3=5 och en från 5 till 5+3=2.
Grafen innehåller alltså bara 3 kanter.
ok! nu fattar jag så det blir
6,2 = 2 sammanhängande komponenter
6,3 = 3 sammanhängande komponenter
6,4 = 2 ammanhängande komponenter
6,5 = 1 sammanhängande komponent
men på b, 1<m<n ger sammanhängande grafer
verkar som att n-m ger antalet sammanhängande komponenter för vissa men inte alla? hur hade du tänkt?
Nä sambandet är inte antal komponenter = n-m.
I en viss graf (n,m) är alla komponenter lika stora?
Om alla komponenter är lika stora så har vi (antalet komponenter) * (storleken på komponenterna)=n.
Så antalet komponenter delar antalet hörn, n.
Så om du tittar på dina resultat för (6,m) kan du lista ut vilken delare det rör sig om?
sven999 skrev:Smutsmunnen skrev:Nej (6,3) har du fått fel,
I (6,3)
Det går en kant från 0 till 0+3=3 och från 3 en till 3+3=0
en kant från 1 till 1+3=4 och en från 4 till 4+3=1.
en kant från 2 till 2+3=5 och en från 5 till 5+3=2.
Grafen innehåller alltså bara 3 kanter.
ok! nu fattar jag så det blir
6,2 = 2 sammanhängande komponenter
6,3 = 3 sammanhängande komponenter6,4 = 2 ammanhängande komponenter
6,5 = 1 sammanhängande komponent
men på b, 1<m<n ger sammanhängande grafer
verkar som att n-m ger antalet sammanhängande komponenter för vissa men inte alla? hur hade du tänkt?
eller är b att dem blir sammanhängande när m<=3?
nja, vet inte riktigt storleken, men menar du t.ex:
6,2 har 2 komponenter, storleken på hörnen är (6+9), då får vi 2*(6+9)?
och på fråga a så blir det väll ingen sammanhängande graf eftersom alla har fler än 1 komponenter?
Nej (6,2) har 2 komponenter, båda innehåller 3 hörn. Så 2*3=6
På samma sätt har (6,3) 3 komponenter, alla tre innehåller 2 hörn. Så 3*2=6.
Så antal komponenter är en delare till antal hörn (=n).
Till exempel om vi tittar på (7,m) utan att rita upp den. Om vi antar att alla komponenter är lika stora, så vet vi att antalet komponenter delar 7, så vi vet att det blir 1 komponent eller 7 komponenter.
Återstår då bara fråga: hur avgöra från m vilken delare till 7?
sven999 skrev:och på fråga a så blir det väll ingen sammanhängande graf eftersom alla har fler än 1 komponenter?
Det stämmer.
Smutsmunnen skrev:Nej (6,2) har 2 komponenter, båda innehåller 3 hörn. Så 2*3=6
På samma sätt har (6,3) 3 komponenter, alla tre innehåller 2 hörn. Så 3*2=6.
Så antal komponenter är en delare till antal hörn (=n).
Till exempel om vi tittar på (7,m) utan att rita upp den. Om vi antar att alla komponenter är lika stora, så vet vi att antalet komponenter delar 7, så vi vet att det blir 1 komponent eller 7 komponenter.
Återstår då bara fråga: hur avgöra från m vilken delare till 7?
är det beroende på storleken på m? annars vet jag inte riktigt
Det är klart att det beror av m.
Om du tittar på dina resultat
(6,2)-> 2 komponenter
(6,3)-> 3 komponenter
(6,4)-> 2 komponenter
(6,5)-> 1 komponent.
Finns det någon känd delarfunktion som ni pratat om på kursen? Som kanske skulle kunna beskriva antalet komponenter?
Smutsmunnen skrev:Det är klart att det beror av m.
Om du tittar på dina resultat
(6,2)-> 2 komponenter
(6,3)-> 3 komponenter
(6,4)-> 2 komponenter
(6,5)-> 1 komponent.
Finns det någon känd delarfunktion som ni pratat om på kursen? Som kanske skulle kunna beskriva antalet komponenter?
Inte vad jag kommer på, på rak arm
sven999 skrev:Smutsmunnen skrev:Det är klart att det beror av m.
Om du tittar på dina resultat
(6,2)-> 2 komponenter
(6,3)-> 3 komponenter
(6,4)-> 2 komponenter
(6,5)-> 1 komponent.
Finns det någon känd delarfunktion som ni pratat om på kursen? Som kanske skulle kunna beskriva antalet komponenter?
Inte vad jag kommer på, på rak arm
vill ju säga n/m men det verkar inte funka?
Det är största gemensamma delaren SGD(n,m).
aha!!!! coolt :D
Så nu har du en hypotes för b)-uppgiften.
Bara bevisa den.
Hint för bevis:
Antag att du börjar i nod nummer r. Därifrån går du till r+m, därifrån till r+2m, därifrån till r+3m osv. Hur lång tid innan du kommer tillbaka dit du började? Antal steg är storleken på varje komponent. När du vet storleken på varje komponent är det lätt att beräkna antal komponenter.
Nice! jag löste den :)
Hur hade du löst denna?
tänker jag rätt om A har 2 och C har 4 sätt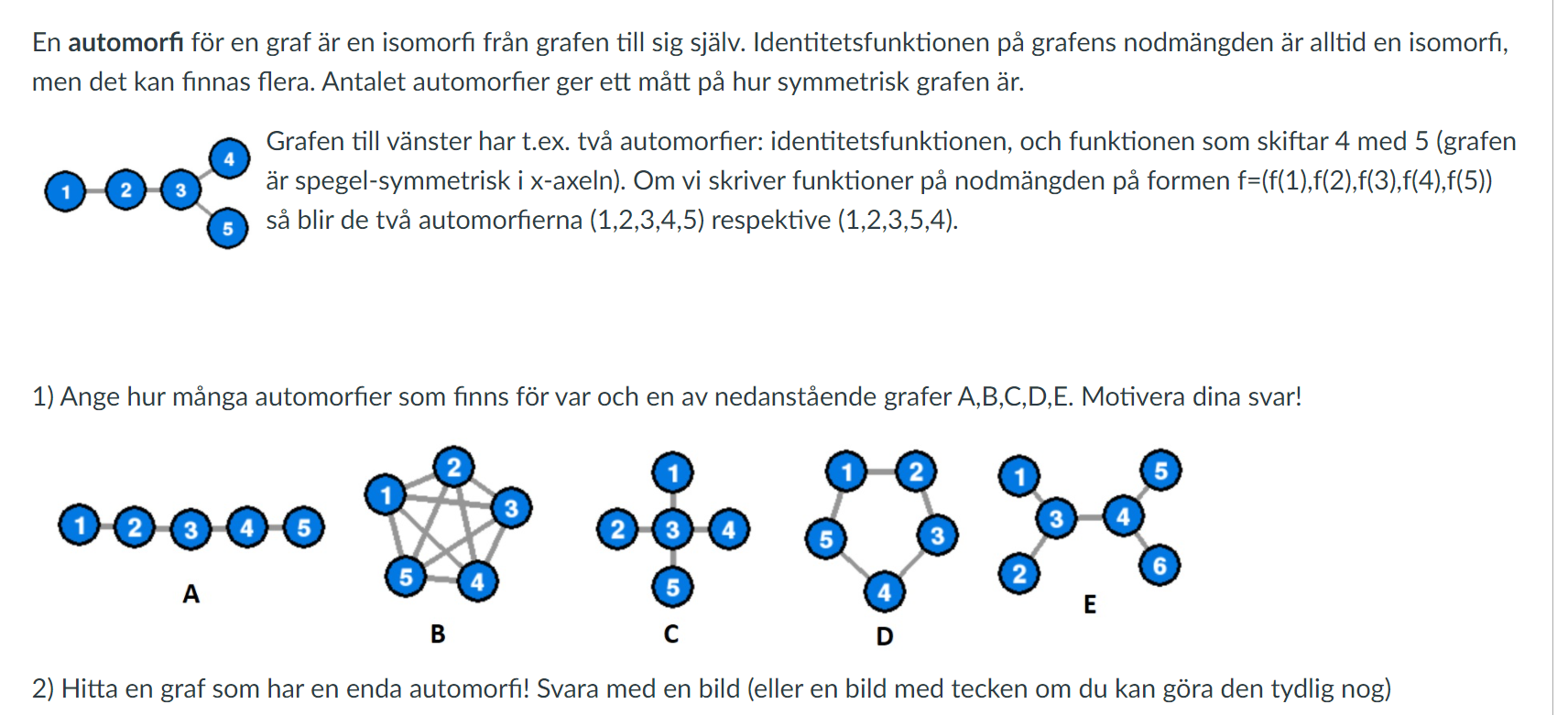
sven999 skrev:Nice! jag löste den :)
Hur hade du löst denna?tänker jag rätt om A har 2 och C har 4 sätt
b och c borde ha 5, och e 4 st?
På b) exempelvis har du helt fel. På c) med. På e) är det inte heller 4.
Försök att tänka utifrån definitionen av automorfism.
Smutsmunnen skrev:På b) exempelvis har du helt fel. På c) med. På e) är det inte heller 4.
Försök att tänka utifrån definitionen av automorfism.
Har du något tips på hur man ska tänka?
sven999 skrev:Smutsmunnen skrev:På b) exempelvis har du helt fel. På c) med. På e) är det inte heller 4.
Försök att tänka utifrån definitionen av automorfism.
Har du något tips på hur man ska tänka?
Börja med b. Den är på sitt sätt lättast. Men den går inte att lösa genom att titta på grafen, man är tvungen att tänka på vad en isomorfi är.
Sedan måste man ha lite olika tricks för olika grafer. Finns ingen enkel, genrell metod för att räkna automorfier.
ok, skulle du kunna ge ett exeempel så jag vet hur jag ska tänka på resten?
Smutsmunnen skrev:sven999 skrev:Smutsmunnen skrev:På b) exempelvis har du helt fel. På c) med. På e) är det inte heller 4.
Försök att tänka utifrån definitionen av automorfism.
Har du något tips på hur man ska tänka?
Börja med b. Den är på sitt sätt lättast. Men den går inte att lösa genom att titta på grafen, man är tvungen att tänka på vad en isomorfi är.
Sedan måste man ha lite olika tricks för olika grafer. Finns ingen enkel, genrell metod för att räkna automorfier.
är det 10 på d, 20 på b?
sven999 skrev:Smutsmunnen skrev:sven999 skrev:Smutsmunnen skrev:På b) exempelvis har du helt fel. På c) med. På e) är det inte heller 4.
Försök att tänka utifrån definitionen av automorfism.
Har du något tips på hur man ska tänka?
Börja med b. Den är på sitt sätt lättast. Men den går inte att lösa genom att titta på grafen, man är tvungen att tänka på vad en isomorfi är.
Sedan måste man ha lite olika tricks för olika grafer. Finns ingen enkel, genrell metod för att räkna automorfier.
är det 10 på d, 20 på b?
10 på d stämmer, 20 på b nej.
Smutsmunnen skrev:sven999 skrev:Smutsmunnen skrev:sven999 skrev:Smutsmunnen skrev:På b) exempelvis har du helt fel. På c) med. På e) är det inte heller 4.
Försök att tänka utifrån definitionen av automorfism.
Har du något tips på hur man ska tänka?
Börja med b. Den är på sitt sätt lättast. Men den går inte att lösa genom att titta på grafen, man är tvungen att tänka på vad en isomorfi är.
Sedan måste man ha lite olika tricks för olika grafer. Finns ingen enkel, genrell metod för att räkna automorfier.
är det 10 på d, 20 på b?
10 på d stämmer, 20 på b nej.
okej! har du något tips på hur jag ska tänka på b c, e?
Smutsmunnen skrev:sven999 skrev:Smutsmunnen skrev:sven999 skrev:Smutsmunnen skrev:På b) exempelvis har du helt fel. På c) med. På e) är det inte heller 4.
Försök att tänka utifrån definitionen av automorfism.
Har du något tips på hur man ska tänka?
Börja med b. Den är på sitt sätt lättast. Men den går inte att lösa genom att titta på grafen, man är tvungen att tänka på vad en isomorfi är.
Sedan måste man ha lite olika tricks för olika grafer. Finns ingen enkel, genrell metod för att räkna automorfier.
är det 10 på d, 20 på b?
10 på d stämmer, 20 på b nej.
borde inte b vara 5! ?
sven999 skrev:Smutsmunnen skrev:sven999 skrev:Smutsmunnen skrev:sven999 skrev:Smutsmunnen skrev:På b) exempelvis har du helt fel. På c) med. På e) är det inte heller 4.
Försök att tänka utifrån definitionen av automorfism.
Har du något tips på hur man ska tänka?
Börja med b. Den är på sitt sätt lättast. Men den går inte att lösa genom att titta på grafen, man är tvungen att tänka på vad en isomorfi är.
Sedan måste man ha lite olika tricks för olika grafer. Finns ingen enkel, genrell metod för att räkna automorfier.
är det 10 på d, 20 på b?
10 på d stämmer, 20 på b nej.
borde inte b vara 5! ?
Ja!

