Stjärna och trianglar?

Det här är en klurig uppgift! Ett sätt att lösa den är att kolla på alla olika trianglar som finns. 
Exempelvis är denna en triangel som finns i stjärnan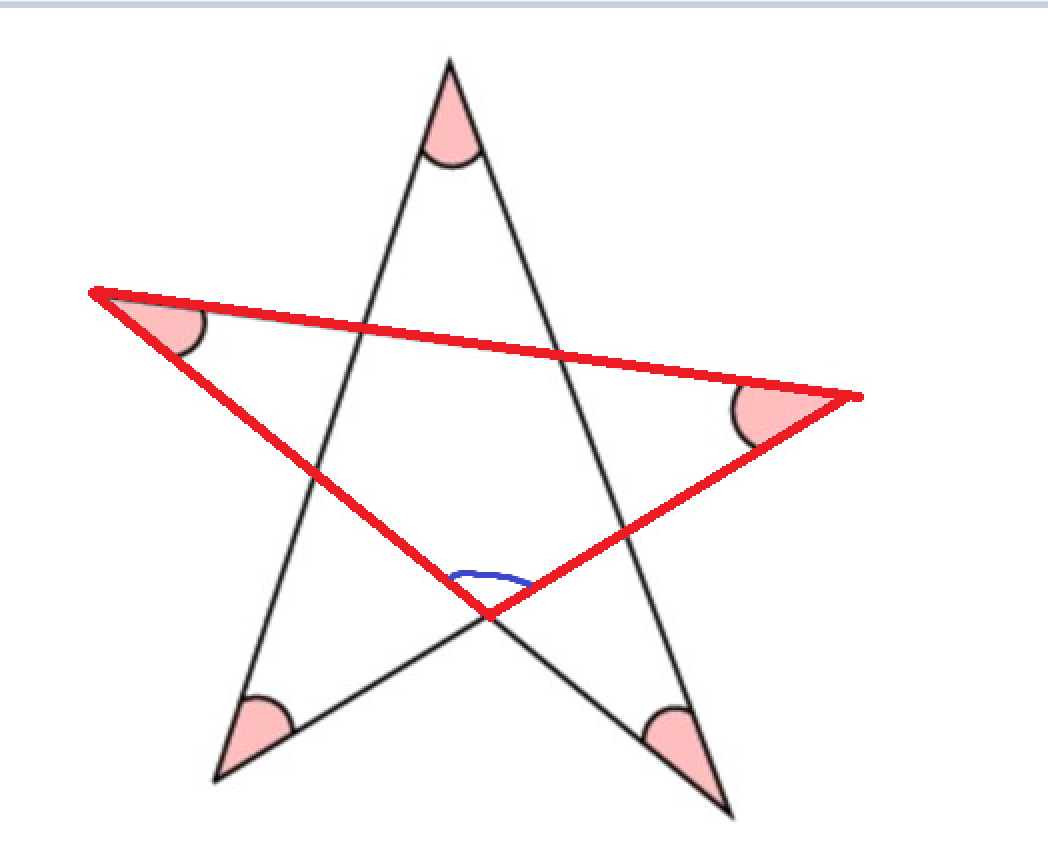

Vad vet vi då om den blåa vinkeln jag ritade ut? Finns det fler trianglar som har vinklar i femhörningen i mitten?

Går det att anta att alla ”röda” vinklar är lika stora?

AlexMu skrev:

Det här är en klurig uppgift! Ett sätt att lösa den är att kolla på alla olika trianglar som finns. 
Exempelvis är denna en triangel som finns i stjärnan

Vad vet vi då om den blåa vinkeln jag ritade ut? Finns det fler trianglar som har vinklar i femhörningen i mitten?

Kalla den blåa vinkel för x:

x>90
180-x=2(röd) <—> 180-2(röd)=x

yttervinkel (av x)=2(röd)

Vi vill ta reda på:

5(röd)=?

EDIT: Det finns flera trianglar att titta på. Varför är de viktiga, kan vi skriva upp fler ekvivalenser då?

Cristian0311 skrev:

AlexMu skrev:

Det här är en klurig uppgift! Ett sätt att lösa den är att kolla på alla olika trianglar som finns. 
Exempelvis är denna en triangel som finns i stjärnan

Vad vet vi då om den blåa vinkeln jag ritade ut? Finns det fler trianglar som har vinklar i femhörningen i mitten?

Kalla den blåa vinkel för x:

x>90
180-x=2(röd) <—> 180-2(röd)=x

yttervinkel (av x)=2(röd)

 

Vi vill ta reda på:

5(röd)=?

Vi kan inte anta att alla röda vinklar är lika stora, men du har rätt ide!

Kan vi bevisa att alla röda vinklar är lika stora genom att rita upp fler trianglar och dra liknande slutsatser?

Själv påstår jag att det går. Men jag är inte helt säker….

Ska rita upp det på ett papper, blir nog tydligare vad jag ska göra :)

Inga vinklar behöver vara lika stora. I figuren är de spetsiga vinklarna ritade olika spetsiga.

AlexMu har förslag på en lösning, jag ett annat.

Kunde inte Cristian fått försöka själv? Vid behov med en liten ledtråd.

Här är en ledtråd till en enklare lösning: titta på en av de små trianglarna och tänk yttervinkelsatsen.

Trinity2 skrev:

 

Varför valde du just den kombinationen av trianglar?

Cristian0311 skrev:

Trinity2 skrev:

 

Varför valde du just den kombinationen av trianglar?

Det passade bra för just denna lösning. 
sedan kan du räkna på antalet rotationer

men jag tycker min första lösning är mera solid. Rotationer kan vara kluriga och det kan lätt bli fel, t.ex. när en cirkel roterar runt en annan cirkel. Hur många varv roterar den egentligen? Här är det enklare eftersom rotationen ej har en ”motyta”. Se gärna på YouTube om exemplet med två mynt. Jag tror det är Numberphile eller något sådant konto.

notera ovan att vi roterar i negativ riktning men jag förkastar detta då det endast är ett tecken som förekommer på bägge sidor om likhetstecknet.

1. Trinity2 skrev:

   Cristian0311 skrev:

   Trinity2 skrev:

    

   Varför valde du just den kombinationen av trianglar?

   Det passade bra för just denna lösning. 
   sedan kan du räkna på antalet rotationer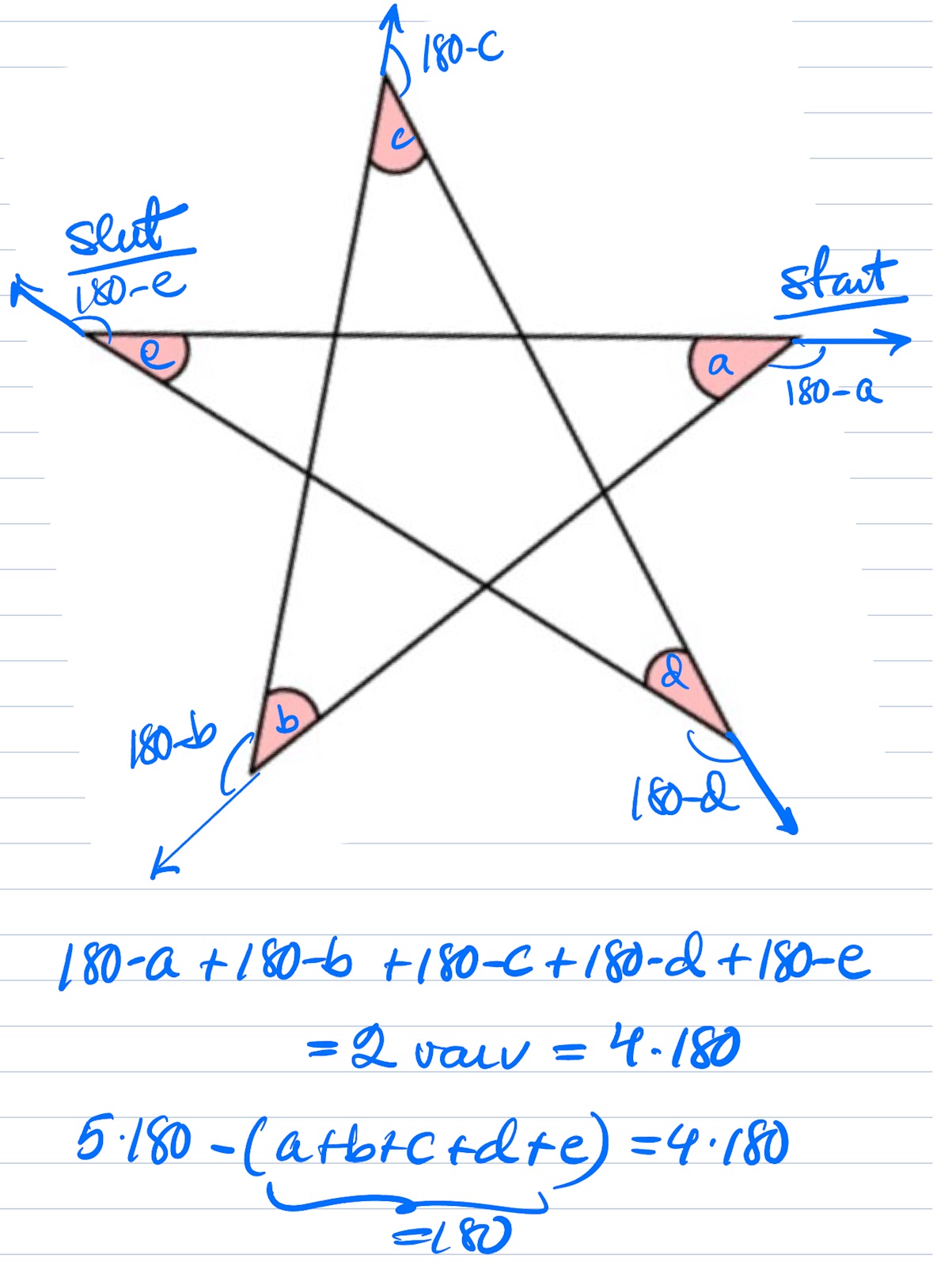

   men jag tycker min första lösning är mera solid. Rotationer kan vara kluriga och det kan lätt bli fel, t.ex. när en cirkel roterar runt en annan cirkel. Hur många varv roterar den egentligen? Här är det enklare eftersom rotationen ej har en ”motyta”. Se gärna på YouTube om exemplet med två mynt. Jag tror det är Numberphile eller något sådant konto.

    

   notera ovan att vi roterar i negativ riktning men jag förkastar detta då det endast är ett tecken som förekommer på bägge sidor om likhetstecknet.

Här är min lösning, hade fullt upp igår (enligt facit var det rätt)….

Hur menar du med rotationer? Vad är det man tittar på då, Trinity?

Var det så du menade Louis? :)

(egentligen går det att ignorera första sidan till viss del, lekte bara lite med uppgiften)

Ytterligare en lösning! Men se uppmaningen i uppgiften: Träna även på att motivera ditt svar.
Du behöver förklara ekvationerna.
Och när du skriver om "yttervinklarna" i svaret verkar du mena något annat än det vedertagna begreppet yttervinkel.

Var det så du menade Louis? :)

Nej, jag menade detta:

Yttervinkelsatsen ger vinklarna a+d (yttervinkel till den färgade triangeln) och b+e.

a + b + c + d + e = 180^o

Svar: Summan av de markerade vinklarna är 180^o.

Här kommer en lösning som inte kräver så mycket räknande.

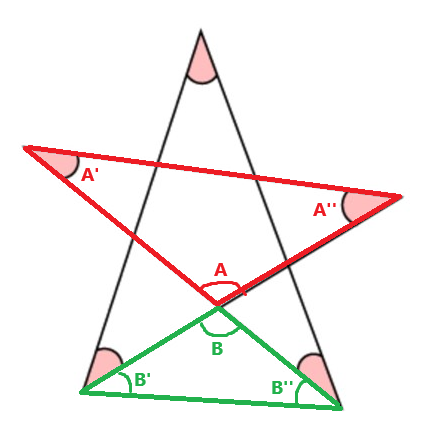
Jag har markerat vinklarna A och B, som förstås måste vara lika stora.

A+A'+A''=180 i den röda triangeln. För den gröna gäller B+B'+B''=180.

Eftersom A=B, så måste A'+A''=B'+B''. 

Vinklarna A' och A'' är tillsammans det som saknas för att kunna bilda en triangel. Vinkelsumman av de markerade vinklarna är 180 grader.

Louis skrev:

Och när du skriver om "yttervinklarna" i svaret verkar du mena något annat än det vedertagna

Du har helt rätt, slarvade lite :(

Var på väg att redigera inlägget, men det var för sent när jag insåg.