Stelkroppsdynamik - svänghjul bromsas
Hej! Jag har fastnat på en uppgift i mekanik. Jag vet inte hur jag ska lösa uppgiften och skulle behöva hjälp med hur jag ska tänka.
Uppgiften lyder:
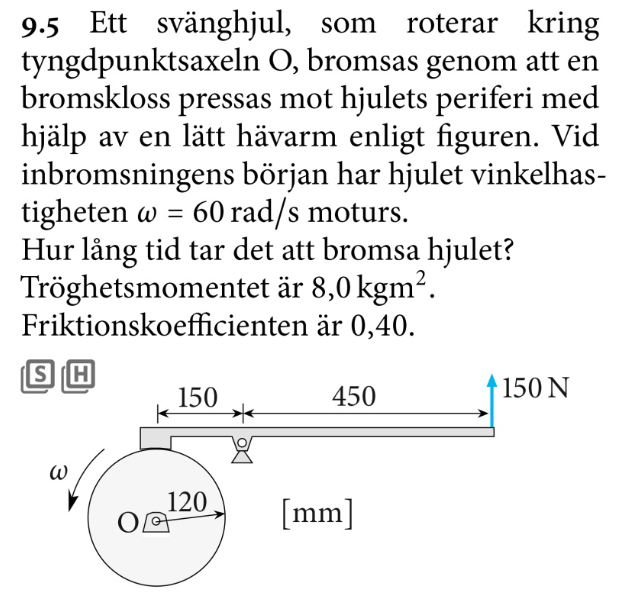
Svaret ska bli 22.2 s.
Jag har frilagt armen och hjulet var för sig och ritat ut krafterna men jag är rätt säker på att jag har gjort fel men jag vet inte hur jag ska ta mig vidare.
För armen tänker jag att krafterna och moment blir (osäker på momentet):
För hjulet tänker jag att krafterna och moment blir (osäker på allt):
Som sagt, jag vet inte hur jag ska gå vidare härifrån. Tacksam för hjälp!
Vilket vridmoment utöver bromsens friktionskraft på hjulet?
Är det kraften som hävarmen utövar på hjulet multiplicerat med radien? Dvs N*r = 150 * 0,12 = 18 Nm
linneak skrev:Är det kraften som hävarmen utövar på hjulet multiplicerat med radien? Dvs N*r = 150 * 0,12 = 18 Nm
Normalkraften utöver inget vridmoment på hjulet (den är ju radiell från rotationscentrum).
Du kan nog rita friktionskraften och du kan nog ett uttryck för den.
Dessutom gör hävarmen att normalkraften på hjulet blir tre gånger så stor.
Friktionskraften är och riktad medurs i det här fallet. Okej så vridmomentet blir ?
linneak skrev:Friktionskraften är och riktad medurs i det här fallet. Okej så vridmomentet blir ?
Ja, förutom att hävstången gör att normalkraften är tre gånger så stor.
I din allra första ekvation har du missat att vridaxeln som hävarmen är fästad i också kan ta en kraft. Det är nog därför du började skriva att normalkraften är 150N.
Hävstångseffekten gör som sagt att normalkraften är tre gånger så stor (momentjämvikt på själva hävarmen).
Ah jag missade vridaxeln... Hävstångseffekten ger alltså 150*0,45 = N*0,15 -> N = 450 N. Vilket ger vridmomentet 0,4*450*0,12 = 21,6 Nm?
Då får jag följande beräkning för hjulmomentet istället:
Eftersom accelerationen och jag vet att ω ska gå från 60 rad/s till 0 så tänker jag att jag borde få fram tiden som . Vilket inte är rätt enligt facit (22,2 s). Vad gör jag för fel?
Tack för era svar!
Jag är själv inte så förtrogen med roterande maskiner men ett alternativ kan vara att räkna med energi istället.
I alla fall blir alfa inte något i m/s2.
Också har i din formel och olika enheter.
Om jag inte har med −rω i momentekvationen så får jag:
Det ger tiden
Vilket är rätt svar. Är detta korrekt uträknat?
Allra först: Vad är det som påverkar hjulets rörelse?
Vinkelhastigheten och bromsklossen?
Nej, det enda som påverkar en kropps rörelse är krafter och moment.
Vilka krafter och moment påverkar hjulets rörelse?
Normalkraften? Vridmomentet och tröghetsmomentet?
linneak skrev:Normalkraften?
Nej, normalkraften i sig påverkar inte rörelsen. Om friktionen vore noll (en bromskloss av smältande is) skulle vi kunna trycka hårt utan att bromsa hjulet.
Vridmomentet
Ja.
och tröghetsmomentet?
Nej, nej. "Moment" är ett knepigt ord. Tröghetsmoment har enhet [kg*m2] och behöver multipliceras med sekund-2 för att få samma enhet som vridmoment, [N*m] = [kg*m2*s-2]
Jag har så svårt för detta.. tack för ert tålamod!
Okej, så hjulets rörelse påverkas av friktionskraften och vridmomentet. Något mer?
linneak skrev:Jag har så svårt för detta.. tack för ert tålamod!
Okej, så hjulets rörelse påverkas av friktionskraften och vridmomentet.
...påverkas av det vridmoment som friktionskraften ger.
Något mer?
Nej, ingenting annat. Vi räknar med att hjulet är perfekt upphängt i sin rotationspunkt, och skulle snurrat i all evighet om vi inte hade bromsat med bromsklossen.
Just det. Tack! Så då är momentekvationen korrekt uppställd?
Och tiden
Jag har inte räknat på rotationer på ganska länge, men jag tycker det ser rätt ut nu.
Okej, tack för all hjälp!


