Statistik - betingad täthetsfunktion hos kontinuerliga S.V

Jag förstår inte beviset (informella?) för betingade täthetsfunktionen av kontinuerliga S.V och har markerat under i bilden steget jag inte förstår.

Om jag utvecklar uttrycket i täljaren med definitionen för fördelningsfunktion av kontinuerliga S.V enligt

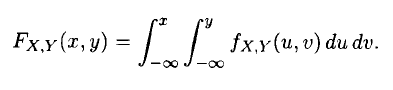
Så får jag nedan. Men jag ser inte hur de förenklat det till den formen de presenterar. Iofs ser jag att deras är bara en approximation, men jag ser fortfarande inte kopplingen mellan formen jag fått jag deras.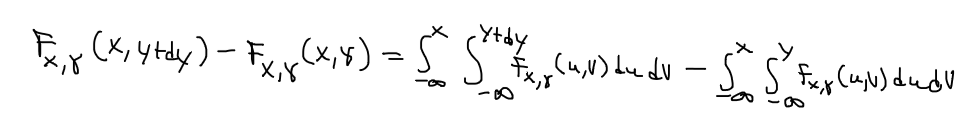

Hej,

defintionsmässigt är

$\frac{δ}{δ y} F_{X, Y} (x, y) = \lim_{d y \to 0} \frac{F_{X, Y} (x, y + d y) - F_{X, Y} (x, y)}{d y}$

För ett mycket litet dy kan vi då approximera

$F_{X, Y} (x, y + d y) - F_{X, Y} (x, y) \approx \frac{δ}{δ y} F_{X, Y} (x, y) d y$

Smutsmunnen skrev:
Hej,

defintionsmässigt är

$\frac{δ}{δ y} F_{X, Y} (x, y) = \lim_{d y \to 0} \frac{F_{X, Y} (x, y + d y) - F_{X, Y} (x, y)}{d y}$

För ett mycket litet dy kan vi då approximera

$F_{X, Y} (x, y + d y) - F_{X, Y} (x, y) \approx \frac{δ}{δ y} F_{X, Y} (x, y) d y$

Okej då är det klart och jag förstår.

Vad hade förresten hänt om man försökt definiera betingade fördelningsfunktionen för X givet att Y=y? Verkar inte hitta så mycket om detta på nätet, de flesta verkar endast ge hur betingade täthetsfunktionen för X givet Y=y ser ut.

Tillägg: 18 okt 2022 17:18

Eller jaha det är väl det som står i beviset: $F_{X|Y=y}(x)$

Svara