Statistik

X är halten (inte i procent) ozon så när du skriver P(X <= 0.95) så frågar du: vad är sannolikheten att halten ozon är under 0.95 mg/m^3? Vilket inte är vad som efterfrågas. 

Okej, ska jag skriva in något annat i x?

Något annat behöver skrivas men vad är jag inte 100% säker på. De efterfrågar ett interval där sannolikheten att det ozonhalten ligger inuti intervallet är 95%. Vi ska alltså bestämma a och b så att P(a <= X <= b) = 0.95. Vi kan tänka oss att intervallet är symmetriskt kring medelvärdet så att a och b är lika långt bort från medelvärdet.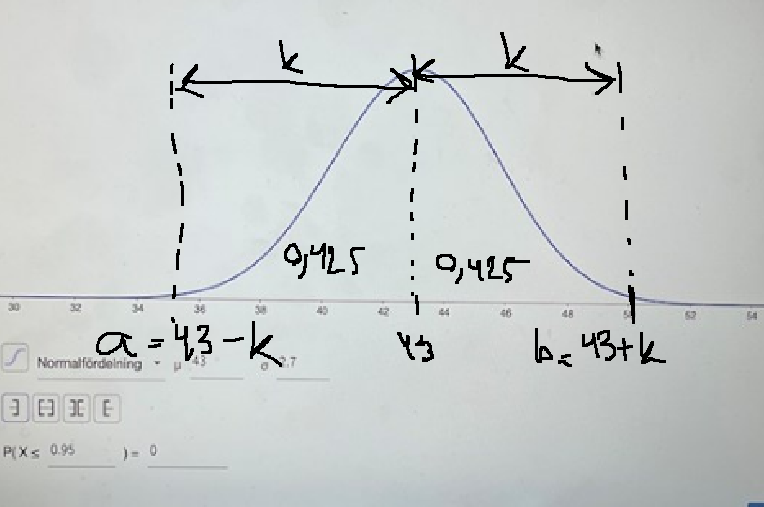

Då kan vi skriva om sannolikheten som P(43 - k <= X <= 43 + k) = 0.95 där 43 - k och 43 + k är intervallets gränser. Det finns kanske någon funktion att bestämma k:s värde i programmet. Annars kan man skriva om uttrycket ytterligare.

Okej tack! Jag ska testa och se!

Jag testade att rita en normalfördelning och sätta ut värdena, nu fick jag rätt svar. Kan man göra såhär? 

Det verkar som du räknat med att ungefär 95% av värdena ligger inom 2 standarsavvikelser från väntevärdet, vilket är en bra approximation.

Generellt får vi ett 95% konfidensintervall genom att använda den 97,5:e percentilen, som för en normalfördelning har värdet 1,96 standarsavvikelser. Så det exakta värdet är aningen mindre än 2. Det betyder att 2,5% av värdena ligger under $\mu - 1.96\sigma$ och 2,5% av värdena över $\mu+1.96\sigma$, och därmed att 95% av värdena ligger i intervallet $[\mu - 1.96\sigma, \mu +1.96\sigma]$.

Detta är väldigt vanligt att räkna med detta värde och förekommer ofta i samband med normalfördelningar.

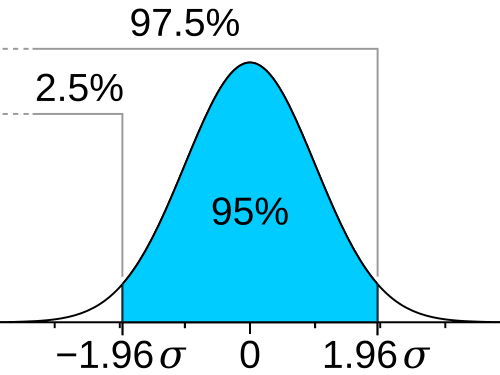
Här är väntevärdet 0.

Bild från https://en.m.wikipedia.org/wiki/97.5th_percentile_point

Av: Cmglee https://commons.m.wikimedia.org/wiki/User:Cmglee

Okej tack så mycket!😊