Stationära processer igenom filter
Hej!
Jag hade behövt hjälp på denna uppgift.
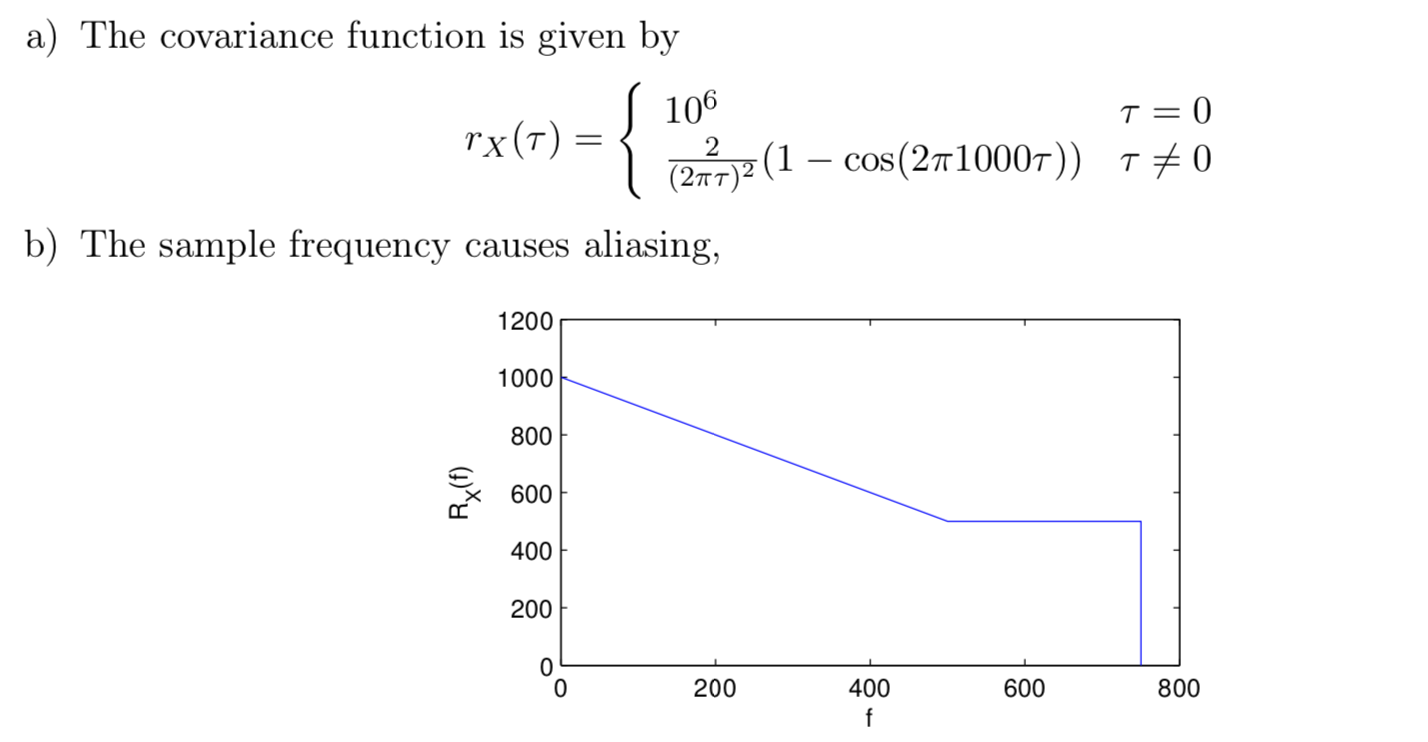
Jag förstår hur man ska beräkna a) och fick samma som i facit med hjälp av formler för fouriertransformer. När det kommer till b) förstår jag dock inte riktigt hur man ska tänka. Förstår att vi inte kan fånga upp någon frekvens större än 750 (1500/2 enligt Nyguist thm of frequency), men förstår inte varför den vid frekvens 500 planar av och är konstant i den nya spectral densityn. All hjälp uppskattas :) 
Det mörkgröna bidraget är invikt. Från vilka frekvenser då?

Ahh tack så jättemycket! Det är frekvenserna upp till 1000 som nu blir uppfångade där istället då.
Nja, jag är inte själv säker på vad som händer här. Men det lilla bidraget vid 501 Hz kan ju inte härröra från 999 Hz (som skulle ge just det bidraget).
Eftersom vi här har både positiva och negativa frekvenser är det väl som vanligt bidraget från en hel samplingsfrekvens bort som vi ser? Det vill säga vårt bidrag vid 501 Hz kommer från -999 Hz, och det större bidraget vid 749 Hz kommer från -751 Hz. Då får vi in hela den verkliga integrerade spektralfrekvensen i [-1000, 1000]Hz in i vårt uppmätta, samplade, frekvensband [-750, 750]Hz.
Hmm nu förstår jag inte helt. Det borde väl komma från både från -999 och 999 i detta fallet då vid 501 Hz?
Nej, du kan inte få ett bidrag från en verklig frekvens som ligger 498 Hz bort, bara från en som ligger 1500 Hz (eller 3000, 4500...) bort.
Jag förutsätter här att mätningen är sådan att vi verkligen ser skillnad på positiva och negativa frekvenser. Det verkar ju så av problemformuleringen att döma - den verkliga signalen innehåller ju negativa frekvenser.

