Stångkraft och förskjutning hållfasthet (Fysik/Universitet)

Aorta skrev:
Jag har kommit fram till förskjutningen för varje stång

De måste vara lika. Är de det i deluppgift a) ?

Jag förstår inte din lösning. Lite text hade nog varit bra för en hållf-okunnig.

Pieter Kuiper skrev:
Aorta skrev:
Jag har kommit fram till förskjutningen för varje stång

De måste vara lika. Är de det i deluppgift a) ?

Det är i båda uppgifterna.

Delta är förlängningen av varje stång. Jag har fått fram att förlängningen på stång 1 (i a-uppgiften) är Fl/AE, men att förlängningen i stång 2 är noll då kraften i stången är noll (S2=0).

Men när du säger det måste ju förskjutningen vara samma för båda då de sitter ihop. Mitt svar på a-uppgiften är korrekt, trots att jag endast räknat ut förlängningen av stång 1. Jag tänker att knutpunkten borde förflytta sig åt höger och neråt. Detta eftersom stång 2 är konstant i längd.

Jag blir förundrad över att förflyttningen i vertikalled är samma som förlängningen av den övre stången eftersom jag som sagt tänkte att den skulle flyttas både neråt och till höger.

Pieter Kuiper skrev:
Aorta skrev:
Jag har kommit fram till förskjutningen för varje stång

Jag förstår inte din lösning. Lite text hade nog varit bra för en hållf-okunnig.

Hur jag har gått till väga är att jag har frilagt punkten och tagit fram stångkrafterna. Med dessa har jag kunnat få fram spänningarna, $σ$ , samt töjningen, $ε$ . Med töjningen har jag sen kunnat få fram själva förlängningen i stängerna.

Jag vet att längden på stång 1 blir $δ + l$ och stång 2 har samma längd efter, alltså $\sqrt{2} * l$ .

Jag vill ha fram förflyttningen av knutpunkten i vertikalled men vet ej hur jag ska få fram det.

Aorta skrev:
förlängningen i stång 2 är noll då kraften i stången är noll (S2=0).

Detta stämmer nog inte helt exakt.

Igen, jag är okunnig inom hållf, har bara lite intuitioner. Och då tänker jag att knutpunkten måste åka ner, för att det hade behövts en likadan diagonalstång på andra sidan för att den vertikala förskjutningen skulle vara exakt noll (symmetri). Och kraften kan vara liten, men inte helt noll.

Men låt oss försumma den (det är nog en andra ordningens effekt). Då rör sig knutpunkten över en cirkel. Och då rör den sig lika mycket nedåt som till höger.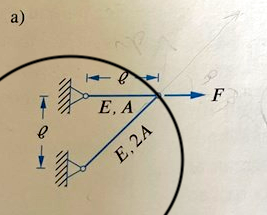

Säg att du har en stång med ändar i A och B. Om vardera änden flyttas ett litet stycke $δ {\vec{r}}_{A}$ respektive $δ {\vec{r}}_{B}$ så ändras stångens längd med $δ = \frac{\vec{A B}}{|\vec{A B}|} ∙ (δ {\vec{r}}_{B} - δ {\vec{r}}_{A})$ .

Tillägg: 5 jun 2024 23:44

Säg att knutpunkten flyttas $δ \vec{r} = (δ x, δ y)$ .

Vi har då S₁l₁/(EA) = $δ_{1}$ = ${\vec{e}}_{x} ∙ δ \vec{r} = δ x$ .

Vidare har vi att 0 = S₂l₂/(2AE)= $δ_{2} = \frac{1}{\sqrt{2}} ({\vec{e}}_{x} + {\vec{e}}_{y}) ∙ δ \vec{r}$ , vilket implicerar att $δ y = - δ x$ .

Det finns många sätt att hantera detta på men jag tycker det enklaste är att rita en figur över deformationen.

Vi vet att den sneda stången inte deformeras något då kraften i den är noll. Här antar vi alltså små deformationer vilket innebär att den statiska friläggningen är konstant över hela förloppet.

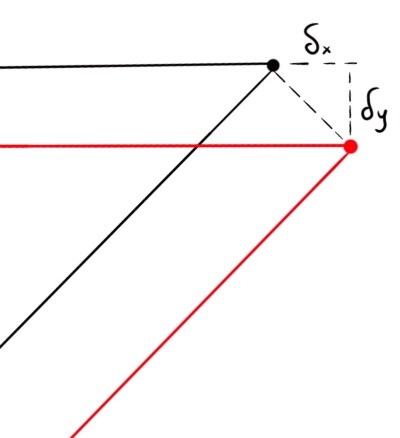
Vi ritar en deformationsfigur där vi zoomar in på knutpunkten. Den horisontella stången dras ut $\delta_1 =\delta_x$ .

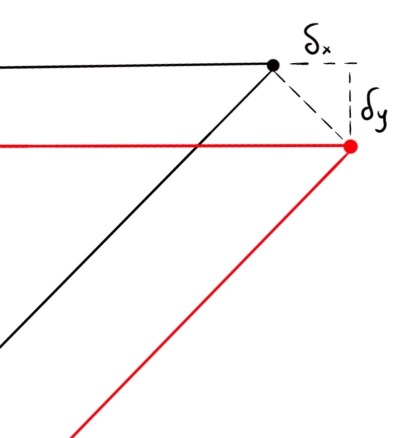
För att den sneda stången ska ha noll deformation $\delta_2=0$ så parallellförflyttar vi den snett nedåt. Då får vi en vertikal förskjutning av knutpunkten lika med $\delta_y$ .

Sedan vet vi från geometrin som bibehålls pga små deformationer att $\delta_x=\delta_y$ .

Hur gick det med denna? Kom du vidare?

PATENTERAMERA skrev:
Säg att du har en stång med ändar i A och B. Om vardera änden flyttas ett litet stycke $δ {\vec{r}}_{A}$ respektive $δ {\vec{r}}_{B}$ så ändras stångens längd med $δ = \frac{\vec{A B}}{|\vec{A B}|} ∙ (δ {\vec{r}}_{B} - δ {\vec{r}}_{A})$ .

Tillägg: 5 jun 2024 23:44

Säg att knutpunkten flyttas $δ \vec{r} = (δ x, δ y)$ .

Vi har då S₁l₁/(EA) = $δ_{1}$ = ${\vec{e}}_{x} ∙ δ \vec{r} = δ x$ .

Vidare har vi att 0 = S₂l₂/(2AE)= $δ_{2} = \frac{1}{\sqrt{2}} ({\vec{e}}_{x} + {\vec{e}}_{y}) ∙ δ \vec{r}$ , vilket implicerar att $δ y = - δ x$ .

Om $δ_{y} = - δ_{x}$ så kan jag få fram förflyttningen i vertikalled (y-led) genom att ta den totala töjningen multiplicerat med cos(45). Jag får då $\frac{F l}{A E \sqrt{2}}$ .Det korrekta svaret är $\frac{F l}{A E}$ så något blir ej rätt.

SaintVenant skrev:
Det finns många sätt att hantera detta på men jag tycker det enklaste är att rita en figur över deformationen.

Vi vet att den sneda stången inte deformeras något då kraften i den är noll. Här antar vi alltså små deformationer vilket innebär att den statiska friläggningen är konstant över hela förloppet.

Vi ritar en deformationsfigur där vi zoomar in på knutpunkten. Den horisontella stången dras ut $\delta_1 =\delta_x$ .

För att den sneda stången ska ha noll deformation $\delta_2=0$ så parallellförflyttar vi den snett nedåt. Då får vi en vertikal förskjutning av knutpunkten lika med $\delta_y$ .

Sedan vet vi från geometrin som bibehålls pga små deformationer att $\delta_x=\delta_y$ .

Är anledningen till att vi parallellförflyttar den utan att ändra geometrin att deformationerna är så pass små?

PATENTERAMERA skrev:
Hur gick det med denna? Kom du vidare?

Jag har lite svårt att greppa själva förflyttningen och tanken med att töjningen blir lika stor i x-riktning som i y tror jag.

Aorta skrev:

Jag får då $\frac{F l}{A E \sqrt{2}}$ .Det korrekta svaret är $\frac{F l}{A E}$ så något blir ej rätt.

Uppgiften är enbart att bestämma den vertikala förskjutningen.

Är anledningen till att vi parallellförflyttar den utan att ändra geometrin att deformationerna är så pass små?

Japp. Pieter förklarade detta ganska bra.

Från din ursprungliga friläggning och kraftjämvikt har du fått fram att kraften i nedre, sneda stången är noll. Om du inte antog små deformationer skulle du tillåta att kraftförhållandet ändras, eftersom geometrin ändras.

Föreställ dig att stängerna är gjorda av gummi och dras på samma sätt. Du har säkerligen en intuition för vad som borde hända då.

Varför är geometrin oförändrad

Om du är intresserad av vad exakt som händer kan jag förklara kort. Det bästa sättet att hantera det på tycker jag är med Maclaurin-utveckling. Du antar en liten störning, och förändring av vinkeln mellan stängerna. Sedan låter du deformationen närma sig noll, gör Maclaurin-utveckling och ser snabbt att inbördes vinkeländring är ordningar närmre noll än deformationen.