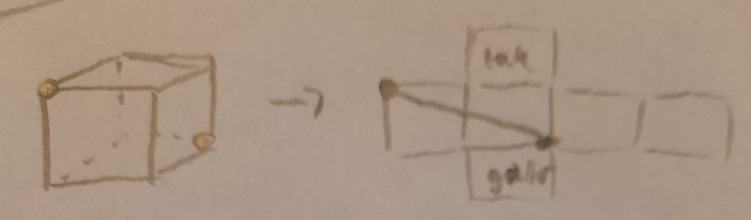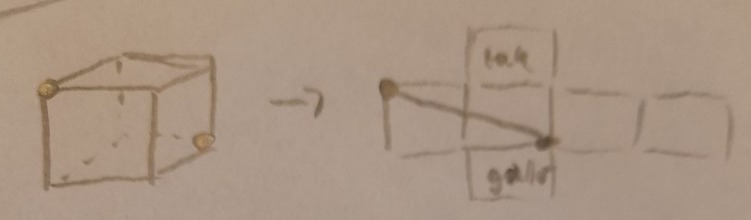Spindel (Pythagoras troligen)

Frågan lyder som följande: Ett rum är 5 m långt, 4 m brett och 3 m högt. Uppe i ena hörnet sitter en spindel. Den får syn på en död fluga i nedre motsatt hörnet. Spindeln beger sig på en promenad ner till flugan. Hur “lång” är den kortaste väg som spindeln kan ta till flugan?

Bara genom att se på figuren förstår man att hypotenusan av åtminstone en triangel ska räknas ut. Jag började med att räkna ut hur lång promenaden skulle bli om man gick bredden först. Alltså 4 m. Sedan skulle han vara tvungen att gå hypotenusan av triangeln med sidorna 5 m och 3 m. Ja då räknar man ut att 5² + 3² = 34 = hypotenusan². Enbart hypotenusan är därför 5.83 m. 4 + 5.83 m får man då = 9.83. Det är sträckan han promenerar om han går “bredden” först. 

Om han går “höjden” först då? Ja då gör han väl det och då blir jag tvungen att räkna… (5 + 4)² = 41. roten ur 41 ≈ 6.4… 6.4 m + 3 m = 9.4 m. Han går höjden först

Om han går längden först… 5 m. (4 + 3)² = 25 roten ur 25 = 5. 5 + 5 m = 10 m därför går han inte längden först… 

Facit säger 8.6 m ? Ska jag räkna med att spindeln kan flyga genom rummet och ta en ännu kortare promenad? Alltså att hypotenusan av triangeln med sidan 3 och hypotenusan av triangeln med längden 5 och bredden 4 räknas? 

Tacksam för svar