Spec. rel. / Dopplereffekt

Om man googlar så hittar man en annan formel.

PATENTERAMERA skrev:

Om man googlar så hittar man en annan formel.

Det är samma formel:

$f_{obs}=\frac{\sqrt {1-(\frac{v}{c})^2}}{1+\frac{v}{c}cos\theta}=(cos\theta =1$ pga.  $\theta -> 0)=\frac{\sqrt {1-(\frac{v}{c})^2}}{1+\frac{v}{c}}$

Med: $f=\frac{c}{\lambda}$

$\frac{c}{\lambda _{obs}}=\frac{c}{\lambda _{source}}\frac{\sqrt {1-(\frac{v}{c})^2}}{1+\frac{v}{c}}<=>\lambda _{source}=\lambda _{obs}\frac{1+\frac{v}{c}}{\sqrt {1-(\frac{v}{c})^2}}=\lambda _{obs}\frac{\sqrt{(1+\frac{v}{c})(1+\frac{v}{c})}}{\sqrt {(1-(\frac{v}{c}))(1+(\frac{v}{c})})}=\lambda _{obs}\frac{\sqrt{1+\frac{v}{c}}}{\sqrt {1-\frac{v}{c}}}$

Så går man härifrån och räknar med formeln två gånger. först våglängden dit, och sedan (efter studs) våglängden tillbaka.

Jag är nu ganska säker på att jag råkat vända på formlerna och skrivit in fel, men mitt svar blir ändå $5.0 nm$. Fortfarande inte rätt. Enligt facit ska svaret vara $85 \mu m$

Du knappar fel någonstans.

Dina indata och dina formler ger ungefär 88 mikrometer.

Bubo skrev:

Du knappar fel någonstans.

Dina indata och dina formler ger ungefär 88 mikrometer.

Såhär:
$\frac{v}{c}=\frac{26.3 \cdot 10^3}{299792458}=8.772735704 \cdot 10^{-5}$
$(\frac{v}{c})^2=(\frac{26.3 \cdot 10^3}{299792458})^2=(8.772735704 \cdot 10^{-5})^2=7.696089 \cdot 10^{-9}$

Rent analytiskt måste det då även gälla att:
$1+8.772735704 \cdot 10^{-5} \approx 1$

och
$1-7.696089 \cdot 10^{-9} \approx 1$

Sedan:

$\frac{\approx 1}{\approx 1}=1 =>$ Kvoten har ingen inverkan på våglängden.

Har även lagt in i MATLAB för att dubbelkolla: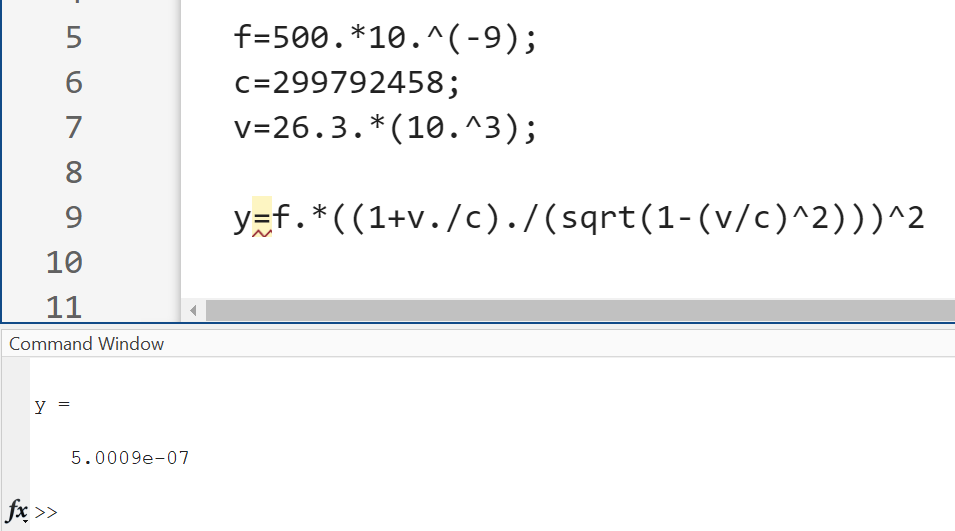

Som uppgiften är formulerad skulle jag tolka den relativa hastigheten (mellan jord och Umami) till <0.0001c. Förstår därmed inte hur det skulle kunna bli en särskilt märkbar relativistisk dopplereffekt.

D4NIEL skrev:

Som uppgiften är formulerad skulle jag tolka den relativa hastigheten (mellan jord och Umami) till <0.0001c. Förstår därmed inte hur det skulle kunna bli en särskilt märkbar relativistisk dopplereffekt.

Jo, så är det väl... Enligt lösningsförslag ska det vara: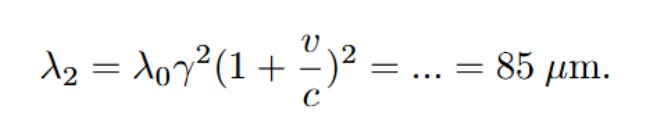

Vilket jag börjar tycka känns mycket konstigt.

Formeln är korrekt tycker jag och det är exakt samma du kom fram till tidigare. Däremot måste ju antingen $\beta$ eller $\lambda_0$ vara något helt annat.

Det kan ju finnas lite tolkningsutrymme kring "våglängden av det mest intensiva ljuset" och kring huruvida jorden rör sig i systemet där solen står stilla, men det kommer bara påverka marginellt. Förstår absolut inte varifrån $85\mathrm{\mu m}$ kommer.

Så här skulle jag räkna ut det (c=1), givet uppgiftstexten:

$\lambda_2=\lambda_0\gamma^2(1+v)^2=\lambda_0\frac{(1+v)(1+v)}{(1+v)(1-v)}=\lambda_0\frac{(1+v)}{(1-v)}\approx \lambda_0$ eftersom

$\gamma=\frac{1}{\sqrt{1-v^2}}\approx 1$eller om man så vill $v\approx 0$

Åt andra hållet blir det analogt

$\lambda_2=\lambda_0\frac{1-v}{1+v}\approx \lambda_0$

D4NIEL skrev:

Formeln är korrekt tycker jag och det är exakt samma du kom fram till tidigare. Däremot måste ju antingen $\beta$ eller $\lambda_0$ vara något helt annat.

Det kan ju finnas lite tolkningsutrymme kring "våglängden av det mest intensiva ljuset" och kring huruvida jorden rör sig i systemet där solen står stilla, men det kommer bara påverka marginellt. Förstår absolut inte varifrån $85\mathrm{\mu m}$ kommer.

Så här skulle jag räkna ut det (c=1), givet uppgiftstexten:

$\lambda_2=\lambda_0\gamma^2(1+v)^2=\lambda_0\frac{(1+v)(1+v)}{(1+v)(1-v)}=\lambda_0\frac{(1+v)}{(1-v)}\approx \lambda_0$ eftersom

$\gamma=\frac{1}{\sqrt{1-v^2}}\approx 1$eller om man så vill $v\approx 0$

Jo, har testat räkna med andra prefix och liknande också, men får inget annat heller. Ingen aning om vad som blir konstigt.

* Edit: tydligen var det tanken att man skulle dra några (ganska konstiga) slutsatser om objektets utseende för att kunna komma fram till svaret, och detta framgick inte i problemställningen. Beklagar detta.

Du får kontakta uppgiftskonstruktören och fråga hur hen tänkt och sedan återkomma. Jag är nyfiken! :)

Det behövs hursomhelst relativa hastigheter mycket nära ljusets (typ 0.988c) för att ge ett så stort rödskift.