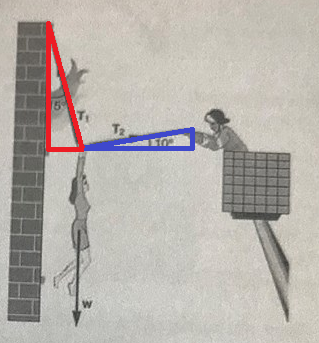
Spännkrafterna
 Kunde jag få hjälp med denna uppgift?
Kunde jag få hjälp med denna uppgift?
Om man följer tipset, och det ska vi göra, måste vi först komposantuppdela T1 och T2
T2 kan delas upp i
- en horisontell komposant riktad åt höger, T2h = T2*cos(10)
- samt en vertikal uppåtriktad T2V = T2*sin(10)
Kan du dela upp T1 på egen hand?
När vi har komposanterna kan vi utnyttja att det råder kraftjämnvikt i bägge led.
Hänger inte med där riktigt. Hur menar du ? Kunde du vissa mig ?
Ture skrev:Om man följer tipset, och det ska vi göra, måste vi först komposantuppdela T1 och T2
T2 kan delas upp i
- en horisontell komposant riktad åt höger, T2h = T2*cos(10)
- samt en vertikal uppåtriktad T2V = T2*sin(10)Kan du dela upp T1 på egen hand?
När vi har komposanterna kan vi utnyttja att det råder kraftjämnvikt i bägge led.
Hänger inte med där riktigt. Kunde du vara snäll och visa mig?
Var hängde du inte med?
Ture skrev:Om man följer tipset, och det ska vi göra, måste vi först komposantuppdela T1 och T2
T2 kan delas upp i
- en horisontell komposant riktad åt höger, T2h = T2*cos(10)
- samt en vertikal uppåtriktad T2V = T2*sin(10)Kan du dela upp T1 på egen hand?
När vi har komposanterna kan vi utnyttja att det råder kraftjämnvikt i bägge led.
Kan du visa mig hur man delar upp T1 är du snäll?
Jag visar hur jag gjorde T2 så ber jag dig försöka göra T1 på egen hand. Om du kör fast så visa i en bild hur du gjort, vad du kommit fram till och var du kör fast.
Jag använder trigonometriska samband i rätvinkliga trianglar
- sin(vinkel) = (motstående katet)/hypotenusa
-cos(vinkel) = (närstående katet)/hypotenusa
Titta på bilden nedan

T2 är hypotenusa i en rätvinklig triangel
T2H är närstående katet till vinkeln som är 10 grader
T2V är motstående katet till vinkeln som är 10 grader.
Sen använder jag det jag skrev ovanför bilden
cos(10) = T2H/T2 , multiplicerar bägge led med högerledets nämnare och får efter förenkling
T2H = T2*cos(10)
T2V tar jag fram på motsvarande sätt men med sin(10) istället
Försök göra på samma sätt med T1
Börja med att rita en triangel!
Ture skrev:Jag visar hur jag gjorde T2 så ber jag dig försöka göra T1 på egen hand. Om du kör fast så visa i en bild hur du gjort, vad du kommit fram till och var du kör fast.
Jag använder trigonometriska samband i rätvinkliga trianglar
- sin(vinkel) = (motstående katet)/hypotenusa
-cos(vinkel) = (närstående katet)/hypotenusaTitta på bilden nedan
T2 är hypotenusa i en rätvinklig triangel
T2H är närstående katet till vinkeln som är 10 grader
T2V är motstående katet till vinkeln som är 10 grader.Sen använder jag det jag skrev ovanför bilden
cos(10) = T2H/T2 , multiplicerar bägge led med högerledets nämnare och får efter förenkling
T2H = T2*cos(10)
T2V tar jag fram på motsvarande sätt men med sin(10) istället
Försök göra på samma sätt med T1
Börja med att rita en triangel!
Jag räknade på de viset:
T1 -T2 = 0 ( pga kraften är horisontell riktning är noll)
sen => T1+T2 - ( 70 kg• 9,82) = 0
T1 = ( 70 • 9,82 ) / 2
T2 = 70 • 9,82 / 2
så T1 = 686,7 N och T2 är 686,7 N
Stämmer det eller inte?
Det är riktigt att summa lrafter är noll i alla riktningar i den punkt personen håller sina händer.
Men för att vi ska kunna räkna ut krafterna i repets båda sidor måste vi först komposantuppdela kraferna i repet så vi får fram krafter som är parallella med och vinkelräta mot tyngdkraften.
Jag visade hur man kan göra med T2.
Försök göra samma sak med T1!
Ture skrev:Det är riktigt att summa lrafter är noll i alla riktningar i den punkt personen håller sina händer.
Men för att vi ska kunna räkna ut krafterna i repets båda sidor måste vi först komposantuppdela kraferna i repet så vi får fram krafter som är parallella med och vinkelräta mot tyngdkraften.
Jag visade hur man kan göra med T2.
Försök göra samma sak med T1!
 Är detta rätt? Menar du så?
Är detta rätt? Menar du så?
Andersson27 skrev:Är detta rätt? Menar du så?
Inte riktigt.
För det första blir det lättare om du ritar triangeln så att vinklarna pekar åt samma håll som i bilden.
Med en spetsig vinkel i toppen, en vinkel rakt under den,
och en liten bas som sticker ur åt höger från -.vinkeln.
Då ser du direkt att är kateten i botten mitt emot den vinkeln,
och är kateten till vänster i anslutning till vinkeln.
Sedan bör du kika igen på de trigonometriska sambanden:
Ture skrev:
sin(vinkel) = (motstående katet)/hypotenusa
cos(vinkel) = (närstående katet)/hypotenusa
Förstår du hur man använder dessa?
jarenfoa skrev:Andersson27 skrev:Är detta rätt? Menar du så?
Inte riktigt.
För det första blir det lättare om du ritar triangeln så att vinklarna pekar åt samma håll som i bilden.
Med en spetsig vinkel i toppen, en vinkel rakt under den,
och en liten bas som sticker ur åt höger från -.vinkeln.
Då ser du direkt att är kateten i botten mitt emot den vinkeln,
och är kateten till vänster i anslutning till vinkeln.Sedan bör du kika igen på de trigonometriska sambanden:
Ture skrev:
sin(vinkel) = (motstående katet)/hypotenusa
cos(vinkel) = (närstående katet)/hypotenusaFörstår du hur man använder dessa?
Förlåt men hänger inte riktigt med 😔, kunde du vissa mig istället?
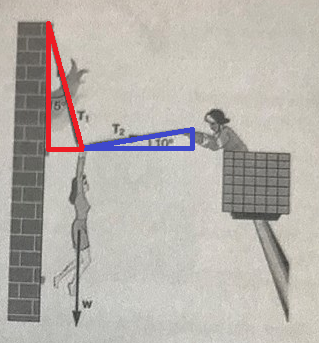
Här har jag ritat in båda trianglarna.
Den blåa är den som Ture redan skissat upp där han döpte sidorna till , och .
(där H betyder horisontell komposant och V betyder vertikal komposant)
Kan du nu på motsvarande sätt döpa sidorna i den röda triangeln?
jarenfoa skrev:
Här har jag ritat in båda trianglarna.
Den blåa är den som Ture redan skissat upp där han döpte sidorna till , och .
Kan du nu på motsvarande sätt döpa sidorna i den röda triangeln?
Är detta rätt? Så menar du?
Nej, har inget med den här triangeln att göra.
De tre sidorna borde heta , och .
Försök igen.
jarenfoa skrev:Nej, har inget med den här triangeln att göra.
De tre sidorna borde heta , och .
Försök igen.
 nu ?
nu ?
Bra!
Nu ska vi ställa upp lite trigonometriska samband mellan , och .
sin(vinkel) = (motstående katet)/hypotenusa
cos(vinkel) = (närstående katet)/hypotenusa
Kan du fylla i dessa uttryck med den vinkel vi har och de rätta sidnamnen?
jarenfoa skrev:Bra!
Nu ska vi ställa upp lite trigonometriska samband mellan , och .
sin(vinkel) = (motstående katet)/hypotenusa
cos(vinkel) = (närstående katet)/hypotenusaKan du fylla i dessa uttryck med den vinkel vi har och de rätta sidnamnen?
Menar du att vi tar :
T1H = T1 • cos 15
T2/ T1 inför sin15
Eller?
Vilken är den 'motstående kateten' i den röda triangeln?
Det är den katet som ligger mitt emot den vinkel vi känner till, d.v.s
Vilken är den 'närstående kateten' i den röda triangeln?
Det är den katet som ligger i nära anslutning till den vinkel vi känner till, d.v.s
Om man sätter in detta i de två trigonometriska sambanden så får man att:
Kan du nu ställa upp motsvarande två uttryck för den blåa triangeln?
jarenfoa skrev:Vilken är den 'motstående kateten' i den röda triangeln?
Det är den katet som ligger mitt emot den vinkel vi känner till, d.v.s
Vilken är den 'närstående kateten' i den röda triangeln?
Det är den katet som ligger i nära anslutning till den vinkel vi känner till, d.v.sOm man sätter in detta i de två trigonometriska sambanden så får man att:
Kan du nu ställa upp motsvarande två uttryck för den blåa triangeln?
T2H = T2 • cos 10
T2v = T2 • sin 10
så eller?
Mycket bra!
Nu är vi redo att ställa upp kraftekvationerna.
I H-led har vi att:
I V-led har vi att:
Om du sätter in alla de trigonometriska sambanden vi just räknat fram,
får du två ekvationer med de två okända spännkrafterna och .
Då kan du äntligen lösa ut dessa.
jarenfoa skrev:Mycket bra!
Nu är vi redo att ställa upp kraftekvationerna.
I H-led har vi att:
I V-led har vi att:
Om du sätter in alla de trigonometriska
sambanden vi just räknat fram,
får du två ekvationer med de två okända spännkrafterna och .
Då kan du äntligen lösa ut dessa.
T1 -T2 = 0 ( pga kraften är horisontell riktning är noll)
sen => T1+T2 - ( 70 kg• 9,82) = 0
T1 = ( 70 • 9,82 ) / 2
T2 = 70 • 9,82 / 2
så T1 = 686,7 N och T2 är 686,7 N
Stämmer det eller inte?
Jag sa att du skulle sätta in de trigonometriska sambanden.
De inkluderar alla sinus och cosinus.
jarenfoa skrev:Jag sa att du skulle sätta in de trigonometriska sambanden.
De inkluderar alla sinus och cosinus.
Men kommer vi få någon siffra utav dem? För de är bara bokstäver tänker jag
sin(15), cos(15), sin(10) & cos(10) är allihop siffror som du behöver för att få denna beräkning att stämma.
jarenfoa skrev:sin(15), cos(15), sin(10) & cos(10) är allihop siffror som du behöver för att få denna beräkning att stämma.
Så dessa sak motsvara väl T2v bara?
Du förstår väl att om:
så betyder det att:
Sinus-funktionen är där av en anledning.
I H-led hade vi alltså kraftekvationen
Här skulle vi sätta in de trigonometriska sambanden:
vilket resulterar i följande kraftekvation för H-led:
Kan du nu sätta in de trigonometriska sambanden i kraftekvationen för V-led?
jarenfoa skrev:Du förstår väl att om:
så betyder det att:
Sinus-funktionen är där av en anledning.
I H-led hade vi alltså kraftekvationen
Här skulle vi sätta in de trigonometriska sambanden:
vilket resulterar i följande kraftekvation för H-led:
Kan du nu sätta in de trigonometriska sambanden i kraftekvationen för V-led?
ja, så nu har vi väl:
cos 15 *sin15*cos10 * sin10 = eller ?
Andersson27 skrev:cos 15 *sin15*cos10 * sin10 = eller ?
Jag är ledsen men jag förstår inte vad du försöker säga här.
Skriv gärna lite längre och berätta hur du tänker.