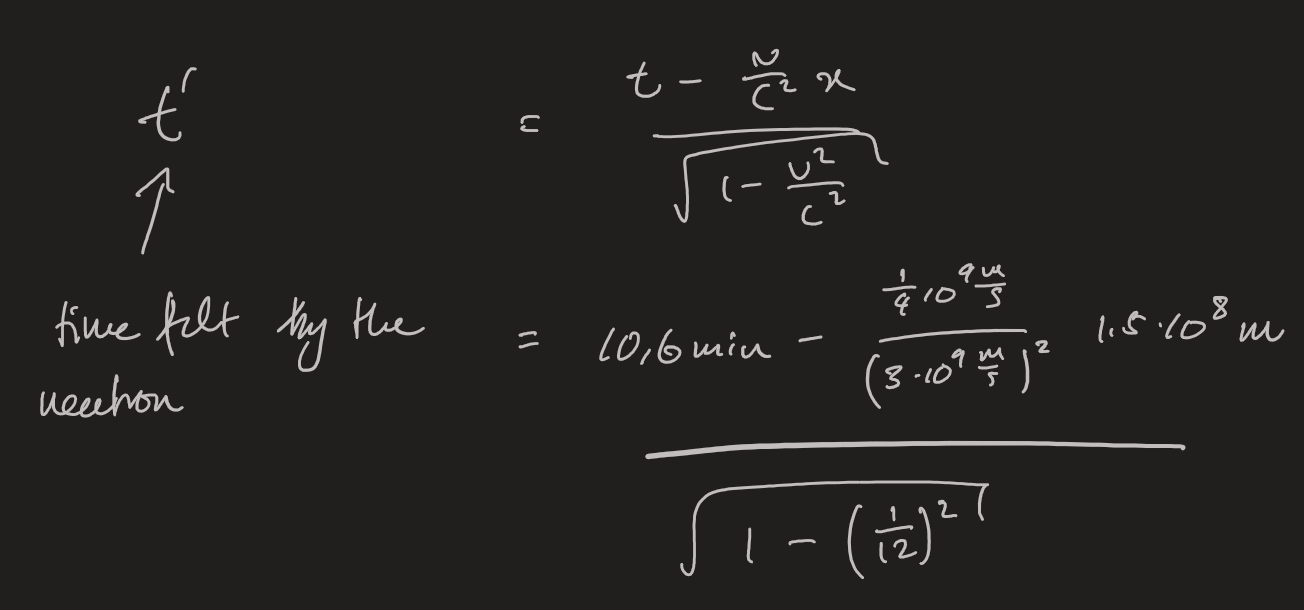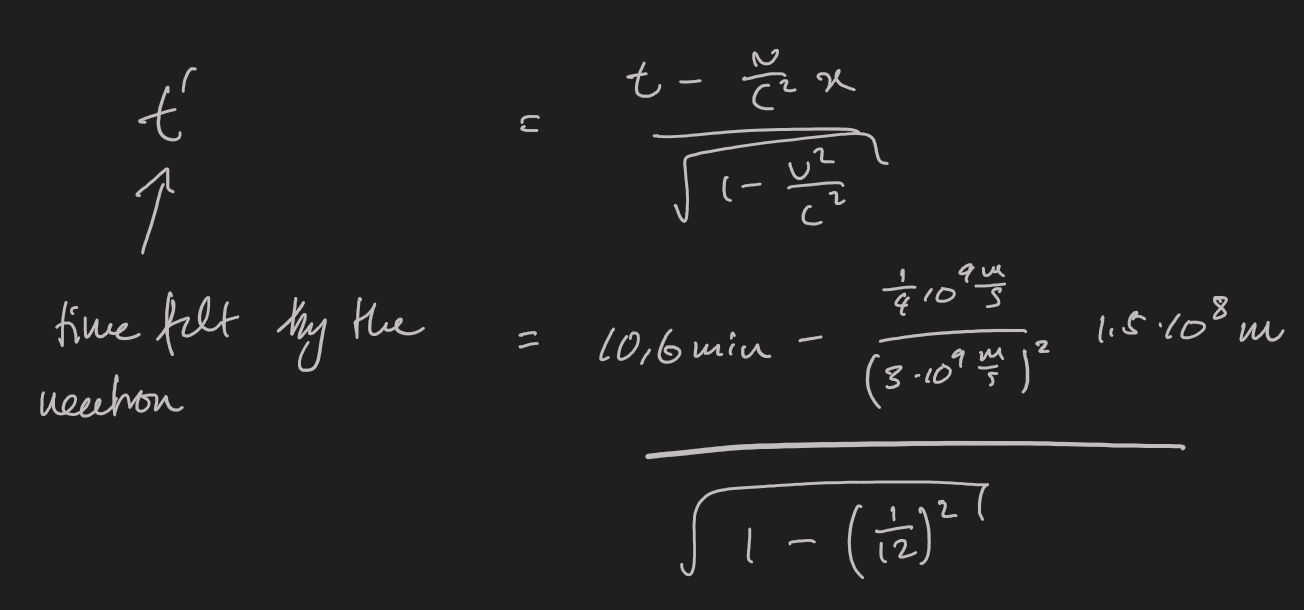Sp. relativitet: göra en fråga med tidsdilatation eller längdkontraktion?
Frågan och lösningen:
Men jag tänkte på ett lite annat sätt. Neutronens upplevda färdtid är lite längre enligt den själv än enligt oss, det är väl rätt? Så neutronerna behöver inte åka med hastigheten v=d/t=1,496*10^8km/10,6min utan lite lägre, nämligen v=d/t' där t'>t är neutronens upplevda färdtid och räknas ut med:
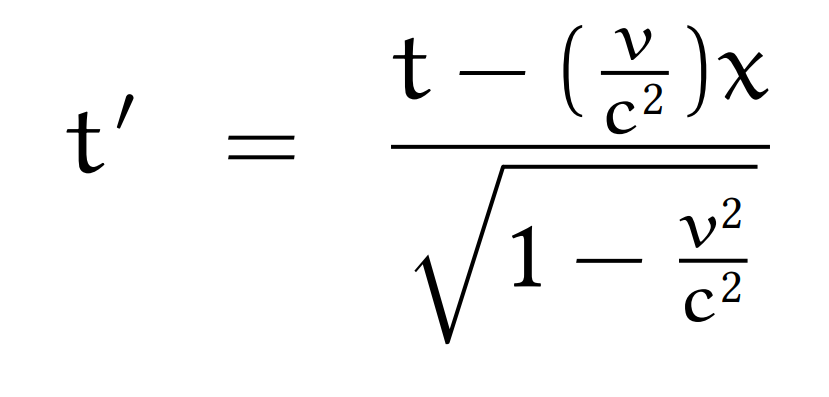
EDIT1: Fast jag tror jag vet vad felet är, det är ju ett grovt cirkelargument eftersom jag använder hastigheten v i den uträkningen vilket jag inte borde veta än. Vad är hastigheten 1,496*10^8km/10,6min egentligen? Är det inte neutronernas hastighet enligt oss på jorden?
EDIT2: Men formeln för v enligt facit innehåller också v, och det är ok?
Nja, neutronens egentid mellan händelsen att den lämnar solen och händelsen att den kommer fram till jorden är mindre än den tid som man på jorden uppfattar att färden tar.
Sätt in t = d/v och x = d i formeln och lös ut v/c i termer av d, c och t’. Sedan om hälften av neutronerna skall komma fram så bör väl t’ sättas lika med halveringstiden.
Det du föreslår, är det annorlunda mot facit? Jag är väldigt förvirrad
Sätt in t = d/v och x = d i formeln
Formeln jag infogade som bild?
och lös ut v/c i termer av d, c och t’. Sedan om hälften av neutronerna skall komma fram så bör väl t’ sättas lika med halveringstiden.
ok...
Jag satte att t är lika med halveringstiden, det är ett till fel jag gjorde i så fall, sjävlklart är det tiden neutronerna känner av som ska vara halveringtid.
Ja, vi ser det i detta fall från en referensram där solen och jorden är i vila, men svaret bör bli det samma.
De ser det från en referensram där neutronen är i vila och solen och jorden rör sig.
Va? Tittar vi inte på en referensram där bara neutronen är i vila?
Hastigheten som frågan efterfrågar, enligt vem är den?
Oprimmat är rumtidkoordinater i referensram där solen och jorden är i vila. Primmat är tiden i en referensram där neutronen är i vila.
I detta fall är v neutronens fart relativt jorden. Jordens fart relativt neutronen är också v. Det blir samma värde.
Qetsiyah skrev:Sätt in t = d/v och x = d i formeln
Formeln jag infogade som bild?
och lös ut v/c i termer av d, c och t’. Sedan om hälften av neutronerna skall komma fram så bör väl t’ sättas lika med halveringstiden.
ok...
Jag satte att t är lika med halveringstiden, det är ett till fel jag gjorde i så fall, sjävlklart är det tiden neutronerna känner av som ska vara halveringtid.
Ja, formeln som du lade in.
Enklast är väl att använda tidsdilatation.
Om tiden för färden är t sett från jorden så är tiden som neutronen uppfattar t’, med sambandet
t = t’.
Om avståndet mellan jorden och solen är d, och neutronens hastighet relativt jorden är v, så gäller det att t = d/v.
d/v = t’/sqrt(1-(v/c)2)
Vilket ger
(v/c)2 = 1/((t’c/d)2+1). Och så väljer vi t’ till halveringstiden.
Du kan även lösa med rumtiddiagram.

Oprimmat är rumtidkoordinater i referensram där solen och jorden är i vila. Primmat är tiden i en referensram där neutronen är i vila.
ok!
I detta fall är v neutronens fart relativt jorden. Jordens fart relativt neutronen är också v. Det blir samma värde.
ok!
PATENTERAMERA skrev:Enklast är väl att använda tidsdilatation.
Om tiden för färden är t sett från jorden så är tiden som neutronen uppfattar t’, med sambandet
t = t’.
Om avståndet mellan jorden och solen är d,
Alltså 1,496*10^8 km som är angivet i uppgiften? Vilket är enligt en obsvervatör på jorden?
och neutronens hastighet relativt jorden är v, så gäller det att t = d/v.
Visst gäller också t'=d'/v?
d/v = t’/sqrt(1-(v/c)2)
Vilket ger
(v/c)2 = 1/((t’c/d)2+1). Och så väljer vi t’ till halveringstiden.
Precis, d är avståndet mellan sol och jord för en observatör som är i vila relativt solen och jorden.
Om vi med d’ menar avståndet mellan sol och jord för en observatör som följer med neutronen så stämmer detta.
Jag förstår och håller med din lösning, men förstår fortfarande inte skillnaden mellan facits och vår lösning.
- Vi använder olika referensramar som du sa.
- De använder t=10.6 men vi använder t'=10.6?
- Facit använder längdkontraktion och vi använder tidsdilatation, gjorde vi/facit så pga referensramarna vi/facit har valt? Dvs det sker ingen längdkontraktion i referensramen vi använder och ingen tidsdilatation i referensramen facit använder?
OK, jag ser nu att de kallar halveringstiden t, vilket skall vara lika med den tid som neutronen uppfattar att färden tar om hälften av neutronerna skall komma fram.
När jag använder t så menar jag tiden för neutronens färd för en observatör på jorden och t' är tiden för färden sett från en observtör som följer med neutronen. Så jag räknar ut v som en funktion av t' och sedan sätter jag t' lika med halveringstiden, och då får man samma resultat som facit.
Vad betyder prim i deras notation?
Om deras referensram följer med neutronen är väl de primmade storheterna enligt stationär observatör på jorden?
Enligt facit så är d’ avståndet mellan jorden och solen enligt en observatör som följer med neutronen, vi får d’ genom längdkontaktion av d (d’ = d/).