Slumpförsök
A och B är två händelser. Vid ett slumpförsök vet man att P(A) = 20 % och
P(B) = 45 % samt att P(A eller B) = 60 %. Beräkna P(A och B).
Ett lätt sätt att lösa denna typ av uppgifter är att använda ett Venndiagram. I mitten är P(A och B). 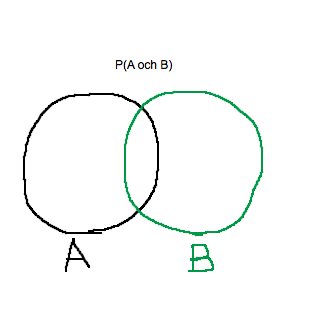
Vi vet att hela A innehåller 20%, och att hela B innehåller 45%. Dessutom ska "Bara A plus Bara B" vara lika med 60%. Hur mycket måste då vara i mitten, för att ekvationen ska gå ihop?
Smutstvätt skrev:Ett lätt sätt att lösa denna typ av uppgifter är att använda ett Venndiagram. I mitten är P(A och B).
Vi vet att hela A innehåller 20%, och att hela B innehåller 45%. Dessutom ska "Bara A plus Bara B" vara lika med 60%. Hur mycket måste då vara i mitten, för att ekvationen ska gå ihop?
är det 5%?
Då skulle vi få 15% i "Bara A", 40% i "Bara B", vilket blir totalt 55%. Alltså måste "A och B"-delen vara något mindre. När vi trycker ihop cirklarna, och därmed ökar "A och B"-delen, subtraheras lika mycket från både "Bara A" och "Bara B". Vi kan alltså skriva det som:
Vi vet också att dessa uttryck tillsammans ska vara 60%. Det ger ekvationen . Kan du ta dig vidare därifrån?


