Skum avslutning på induktion - har GPT rätt?
 Min sista rad:
Min sista rad:
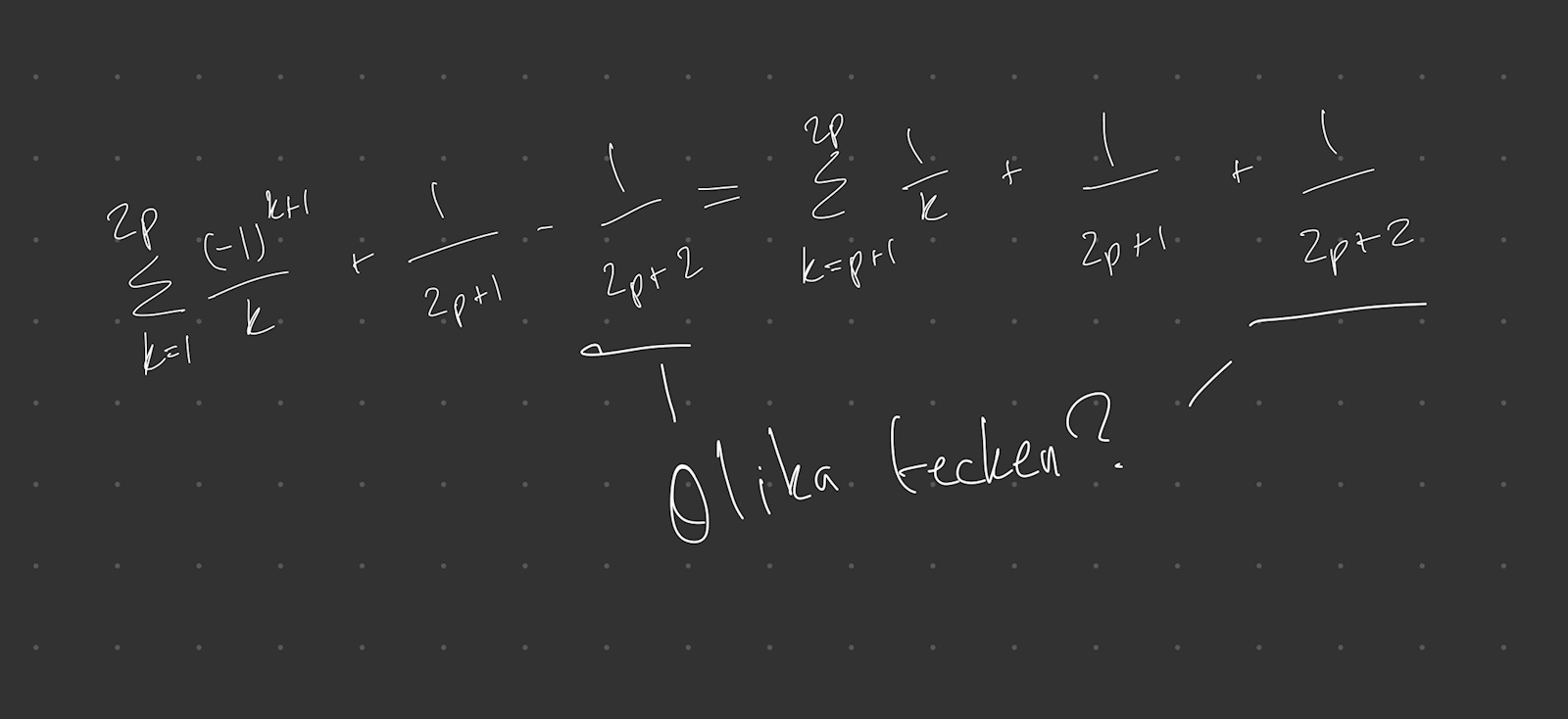 Detta tycker GPT håller för induktionsbeviset trots olika tecken. Någonting om att summans termer skiftar tecken och att något händer då man sätter p+1. Men förstod inte riktigt. Någon som som skulle vilja förklara?
Detta tycker GPT håller för induktionsbeviset trots olika tecken. Någonting om att summans termer skiftar tecken och att något händer då man sätter p+1. Men förstod inte riktigt. Någon som som skulle vilja förklara?
(skriv gärna om ni vill ha GPT:s svar eller hela min lösning)
Skulle du kunna visa hela din lösning? Och vad är er konvention för de naturliga talen? Inkluderas ?

Oklart om du kan se. 0 inkluderas ej.
Likheten stämmer inte.
På högerledet har du lagt till 1/(p+1) men du har inte kompenserat för det, så .
Om man dessutom lägger till så kommer beviset funka och man får rätt tecken framför 1/(2p+2).
Just det, jag bara adderade på den för att det skulle passa men glömde att dra bort den igen..😭🫠
Du är fantastisk. Tack.🙏
(GPT förde mig på konstiga villovägar.🥲)
Som ibland nämns här på forumet: ChatGPT är bra på lingvistiska uppgifter, inte så bra på matematik. I slutändan är det bara en statistisk modell.
naytte skrev:Som ibland nämns här på forumet: ChatGPT är bra på lingvistiska uppgifter, inte så bra på matematik. I slutändan är det bara en statistisk modell.
Ja, den är duktig på viss programmering och jag tänkte att induktionsbevis typ är liknande struktur. Men hade ju uppenbarligen fel.



