Skulle det gå att lösa denna uppgift på ett specifikt sett.
Skulle man med hjälp av trigonometri, räkna ut vinkeln på toppen i ett två dimitionelt perspektiv, som en triangel, Sedan skapa en ekvation, som beteer sig som en parabel, med hjälp av vinkeln. Sedan tänka sig cylinder i 2d, som en rektangel, och att den har två hörn fäst vid linjen, och två nedre hörn vid r axeln, Då vet vi att den undre sidan är 2r lång, och längden är h värdet på ekvationen, då ersätter vi bara r i h form, sedan deriverar vi efter maxim-punkten på ekvationen, där ifrån får vi vårt h värde, sedan sätter vi in det värdet i vår formel och får även tag på r värdet. Sedan tar vi r^2*pi*h, får ut största möjliga volymen?
Jag är inte helt med på vad du menar.
Testa. Vilken volym får du?
Det är nog delvis rätt. Om du ska maximera volymen så är det formeln för volymen du ska derivera, jag är inte säker på vad du deriverar nu.
Jag vet inte vad det är för parabel du tänker på. Skriv allt matematiskt så får vi se.
Laguna skrev:Det är nog delvis rätt. Om du ska maximera volymen så är det formeln för volymen du ska derivera, jag är inte säker på vad du deriverar nu.
Jag vet inte vad det är för parabel du tänker på. Skriv allt matematiskt så får vi se.
Hur skulle ni löst den?
Genomför det du har skrivit så får vi se.
AlexanderJansson skrev:Laguna skrev:Det är nog delvis rätt. Om du ska maximera volymen så är det formeln för volymen du ska derivera, jag är inte säker på vad du deriverar nu.
Jag vet inte vad det är för parabel du tänker på. Skriv allt matematiskt så får vi se.
Hur skulle ni löst den?
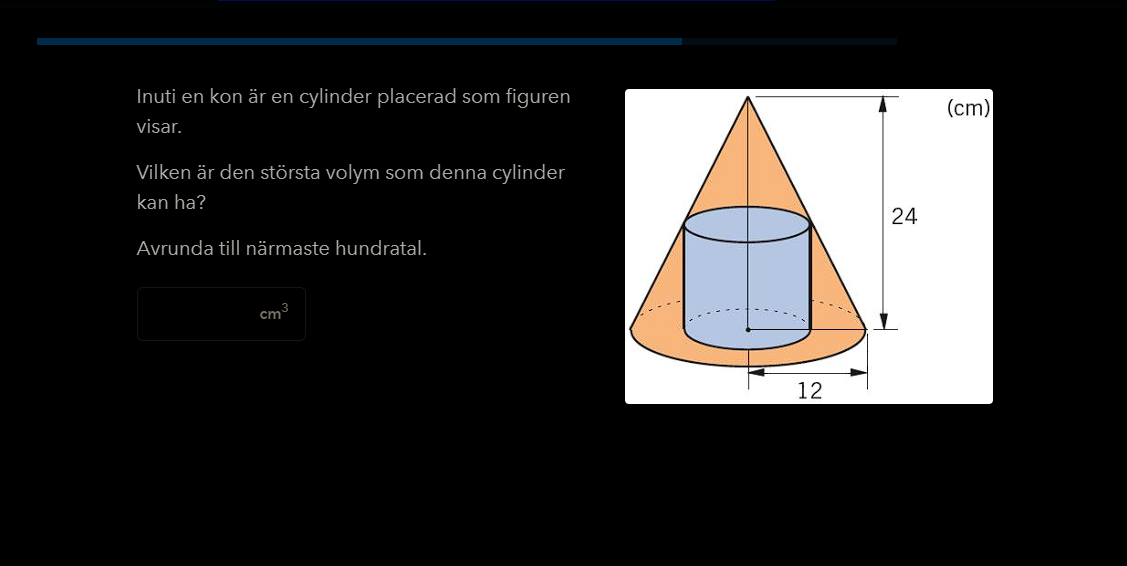
Börja med att konstatera att om radien för cylindern är r, så är h =24-2r. Skriv volymen som en funktion av r, derivera och så vidare.
Laguna skrev:Genomför det du har skrivit så får vi se.
Tillägg: 19 feb 2023 23:02
Fel svar...
Tillägg: 19 feb 2023 23:02
Öppna bild i ny flik och zooma
AlexanderJansson skrev:
Jag tror det blev onödigt krångligt där. Det behövs ingen trigonometri för att lösa uppgiften om du istället använder Smaragdalenas tips.
För att komma fram till det kan du använda likformighet, se bild.
Den stora triangeln har dubbelt så stor höjd () som bas (). Alltså måste även den lilla triangelns höjd vara dubbelt så stor som dess bas . Därav .
Cylinderns volym blir då .
Kommer du vidare därifrån?
Korrigerade ett par skrivfel i föregående svar.
