Skriva vektor som en summa w = u + v
Låt L vara linjen x+ 2y = 0
Skriv vektorn w = (-4,7) som en summa w = u + v, där u är parallell med L och v är vinkelrät mot L.
Jag vet inte hur jag bör dela upp u och v får att få det två linjerna, om det finns något speciellt sätt att tänka eller så.
//Nisse33
Vad blir riktningsvektorn för linjen? kommer att vara en multipel av denna.
Kan du finna en vektor som är vinkelrät mot linjen? I så fall kommer att vara en multipel av denna vektor.
AlvinB skrev:Vad blir riktningsvektorn för linjen? kommer att vara en multipel av denna.
Kan du finna en vektor som är vinkelrät mot linjen? I så fall kommer att vara en multipel av denna vektor.
Fick fram genom att ta 1(x-(-4))+2(y-(7)) = x+2y-10 = 0
Men hur ska jag få fram den vinkelräta vektorn till linjen som går mot punkten?
Du har två sätt att ta fram en vinkelrät vektor:
- Utnyttja att två linjer är vinkelräta om deras -värden har produkten .
- Utnyttja att två vektorer är vinkelräta om deras skalärprodukt är noll.
Hej!
Din vektor kan skrivas som summan
där betecknar ortogonal projektion på (denna vektor är parallell med ) och betecknar ortogonal projektion på (denna vektor är vinkelrät mot ) där är det ortogonala komplementet till linjen .
så för att lösa
vad ska jag kalla som är en linje och inte en vektor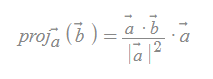
och sen vilken formel bör jag använda för att lösa


