Skriva vektor som en summa w = u + v

Vad blir riktningsvektorn för linjen? $u$ kommer att vara en multipel av denna.

Kan du finna en vektor som är vinkelrät mot linjen? I så fall kommer $v$ att vara en multipel av denna vektor.

AlvinB skrev:

Vad blir riktningsvektorn för linjen? $u$ kommer att vara en multipel av denna.

Kan du finna en vektor som är vinkelrät mot linjen? I så fall kommer $v$ att vara en multipel av denna vektor.

Fick fram $u$ genom att ta 1(x-(-4))+2(y-(7)) = x+2y-10 = 0

Men hur ska jag få fram den vinkelräta vektorn till linjen som går mot punkten?

Du har två sätt att ta fram en vinkelrät vektor:

1. Utnyttja att två linjer är vinkelräta om deras $k$-värden har produkten $-1$.
2. Utnyttja att två vektorer är vinkelräta om deras skalärprodukt är noll.

Hej!

Din vektor kan skrivas som summan

    $w = \text{proj}_L(w) + \text{proj}_{L^{\perp}}(w)$

där $\text{proj}_{L}$ betecknar ortogonal projektion på $L$ (denna vektor är parallell med $L$) och $\text{proj}_{L^{\perp}}$ betecknar ortogonal projektion på $L^{\perp}$ (denna vektor är vinkelrät mot $L$) där $L^{\perp}$ är det ortogonala komplementet till linjen $L$. 

så för att lösa  $w=projL\left(w\right)+projL\perp \left(w\right)$

vad ska jag kalla $a$ som är en linje och inte en vektor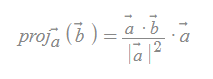

och sen vilken formel bör jag använda för att lösa $projL\perp \left(w\right)$