Skriva tal som produkt av primtal
Hej! Hur ska jag tänka när jag ska skriva 209 som en produkt av primtal? Talen jag skulle göra detta på innan var 45, där jag direkt såg att det var 3 x 3 x 5, samt 105, och där tänkte jag att 105 går att dela på 5, vilket = 21. Och då blir det 21 x 5 = 7 x 3 x 5. Men det känns inte alls lika lätt när det är ett större tal som 209 där det dessutom inte går att dela talet. Kan någon hjälpa mig med tricket/tricken för att klura ut svaret, då det inte är särskilt tidseffektivt att sitta och multiplicera massa slumpmässiga tal med varandra tills det att man kommer fram till rätt svar. Tack på förhand!
Hjalpmaj skrev:Hej! Hur ska jag tänka när jag ska skriva 209 som en produkt av primtal? Talen jag skulle göra detta på innan var 45, där jag direkt såg att det var 3 x 3 x 5, samt 105, och där tänkte jag att 105 går att dela på 5, vilket = 21. Och då blir det 21 x 5 = 7 x 3 x 5. Men det känns inte alls lika lätt när det är ett större tal som 209 där det dessutom inte går att dela talet. Kan någon hjälpa mig med tricket/tricken för att klura ut svaret, då det inte är särskilt tidseffektivt att sitta och multiplicera massa slumpmässiga tal med varandra tills det att man kommer fram till rätt svar. Tack på förhand!
Man får prova sig fram på ett systematiskt sätt.
Det finns ingen generell metod att primtalsfaktorisera ett tal utan man provar från 2 och uppåt till dess att man antingen hittat en faktor eller kommit fram till roten ur talet.
Ett exempel: Vi vill hitta primtalsfaktorerna till 77, roten ur 77 är ungefär 8,8 alltså måste v testa med primtalen som finns mellan 1 och 8 för att hitta faktorer
77/2 = 38,5, nej 2 är ingen faktor
77/3 = 25,66... nej, 3 är ingen faktor
77/5 = 15,4 nej ingen faktor
77/7 = 11, ja, 7 är en faktor och uppenbarligen även 11. Då måste vi kolla om 11 har några primtalsfaktorer, (men det kan vi säga direkt att det inte har eftersom vi redan testad med talen 2 till 7 och roten ur 11 är cirka 3,1)
Man kan givetvis förenkla lite grann, vi ser direkt om talet är jämnt, då är 2 en faktor, om siffersumman är 3, då är tre en faktor, om talet slutar på 5 eller 0 då är 5 en faktor osv.
I ditt exempel 209 måste du alltså testa alla primtal från 2 tom 13 ()
Jag hade använt reglerna för delbarhet. För 2 gäller det att talet är jämnt, 3 så skall siffersumman vara delbar med 3 ich samma gäller 9. 4 skall de 2 sista talen vara delbara med 4, 5 så skall talet sluta på 0 eller 5. Osv.
Som Dracaena säger är delbarhetsreglerna väldigt användbara till detta. Men ibland, som för mig med 209, behöver man prova fler primtal än man minns regler för. Så här går jag till väga på 209, när jag undersöker ett primtal i taget:
2: 209 är udda, så det är inte delbart med 2
3: Beräkna siffersumman: 2+0+9 = 11, vilket inte kan delas med 3 (så då kan 209 inte heller det)
5: 209 slutar inte på 0 eller 5, och kan därför inte delas med 5
7: Minns inte regeln, så jag letar efter multipel av 7 som ligger nära 209. Notera att 7*3 = 21, och 21*10 = 210 vilket är nära 209. Men 210 är alltså en multipel av 7, och 209 ligger bara 1 steg därifrån (inte 7 eller en multipel av 7), så 209 är inte delbart med 7.
11: Minns inte regeln, så letar efter en multipel igen. 11*10 = 110, och sen 110*2 = 220. Så 220 är en multipel av 11, och det råkar ligga exakt 11 steg från 209. Därför är även 209 delbart med 11.
209 / 11 = 19, och eftersom 19 också är ett primtal är vi klara: 11*19.
Det finns delbarhetsregler även för 7 och 11, om man vill kan man lära sig dem med. Men det är bra att ha en backup-plan, för de fall då inga låga primtal funkar =)
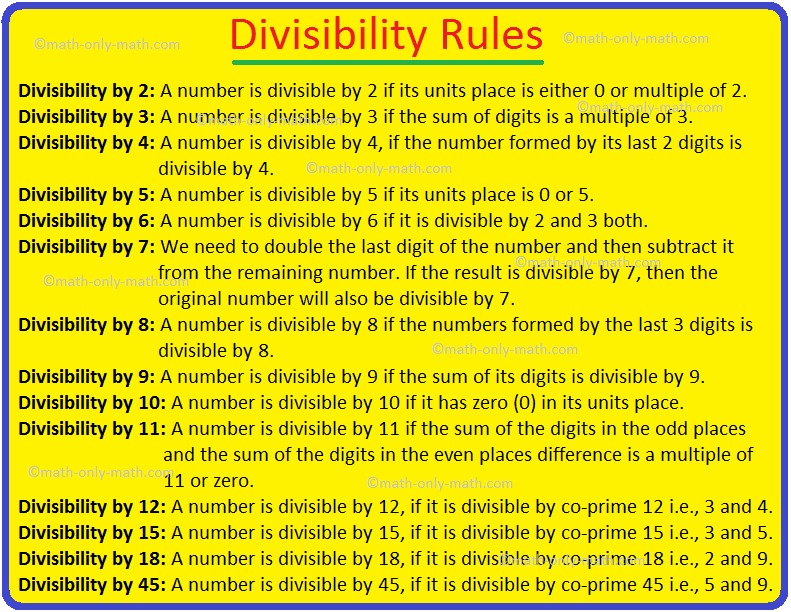
Här har vi en lista! @Skaft, jag slutade vid 5 eftersom jag själv inte hade 7,11 osv på minnet hehe.




