Skriv z i form re^iv
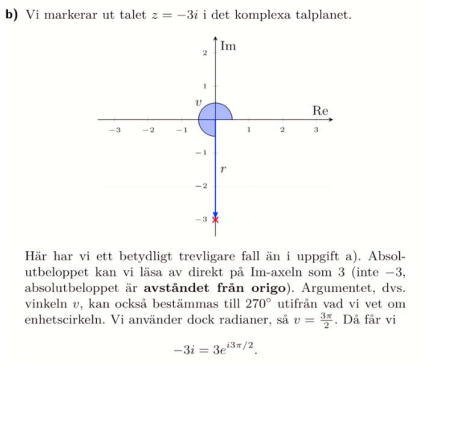 Skriv z i formen re^iv där r= z-absolutbellepp
Skriv z i formen re^iv där r= z-absolutbellepp
z=-3i
Jag hänger in med hur facit kommer fram till v=0.86
och hur de får fram 
micke2z skrev:
Skriv z i formen re^iv där r= z-absolutbellepp
z=-3i
Jag hänger in med hur facit kommer fram till v=0.86
och hur de får fram
Nu handlar det om en helt annan ekvation än den översta, nämligen . En sådan ekvation är betydligt enklare att lösa om vi har högerledt i polär form istället. Då behöver vi dels räkna ut avståndet från origo till punkten i det komplexa talplanet, dels vinkeln mellan positiva realaxeln och en linje från origo till punkten. Avståndet (absolutbeloppet) beräknar vi med hjälp av Pytahagoras sats (), vinkeln får vi med hjälp av arc tan.
ok, då förstå jag hur man löser r och v. Men mitt tröga arsle vet inte hur man fick fram 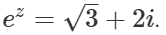 de värdena från -3i
de värdena från -3i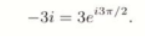 för vi vet att im ligger -3i
för vi vet att im ligger -3i
Men nu blir detta 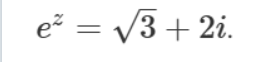
Det gäller väl två olika ekvationer?
Till vilken uppgift hör facit?
 7275 b)
7275 b)
5275 b handlar om att skriva om z = -3i på polär form.
Den del av facit du visade från början (med roten ur 7 osv) verkar höra till 5276 b.
Två olika uppgifter alltså.
Yngve skrev:5275 b handlar om att skriva om z = -3i på polär form.
Den del av facit du visade från början (med roten ur 7 osv) verkar höra till 5276 b.
Två olika uppgifter alltså.
ah. Nu låter det helt rimligt. Mitt fel, tack för hjälpen.





