13 svar

78 visningar

naytte behöver inte mer hjälp

Skriv om funktionen till en cosinusfunktion

Skriv om funktionen $\displaystyle f(x)=-3\sin x +\sqrt{5}\cos x$ som en cosinusfunktion.

Min ansats:

Antag att funktionen kan skrivas på formen $\displaystyle f(x)=A\cos(x-b)$ . Då kommer

$\displaystyle A=\sqrt{(\sqrt{5})^2+(-3)^2}=\sqrt{14}$ .

Detta låter en då göra en omskrivning:

$\displaystyle f(x)=\sqrt{14}(-\frac{3}{\sqrt{14}}\sin x +\frac{\sqrt{5}}{\sqrt{14}}\cos x)$ .

Om vi tänker på utvecklingen av $\displaystyle \cos(x-b)$ blir den $\displaystyle \cos x\cos b +\sin x \sin b$ . Då kan vi dra följande slutsats:

$\{\begin{cases} \cos b = \frac{\sqrt{5}}{\sqrt{14}} \\ \sin b = - \frac{3}{\sqrt{14}} \end{cases}$

Om vi tittar i enhetscirkeln:

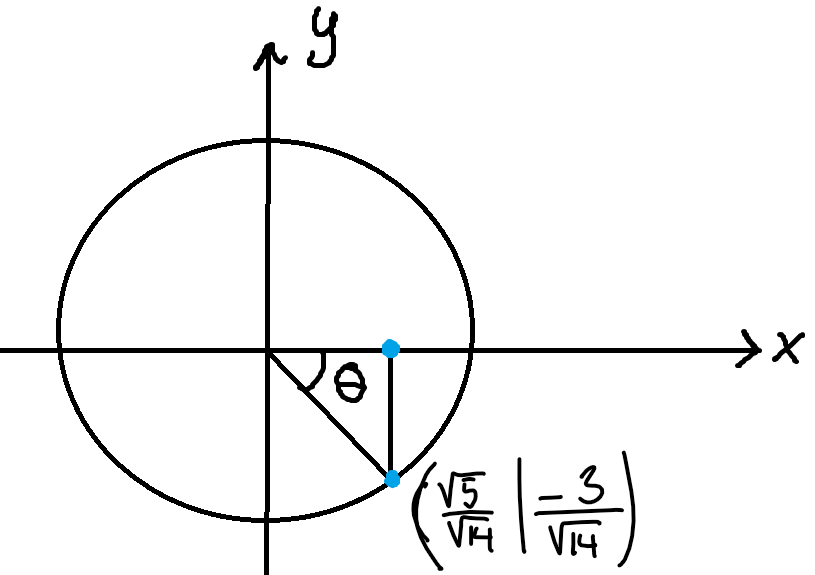
Nu är det enkelt att se att vinkeln som ska leverera denna punkt är:

$\displaystyle b=2\pi-\arctan(-\frac{3}{\sqrt{5}})$

Problemet är nu att när jag stoppar in allting i min cosninusfunktion blir det "rätt" graf men den är felaktigt förskjuten:

$\displaystyle f(x)=\sqrt{14}\cos(x-(2\pi-\arctan(-\frac{3}{\sqrt{5}})))=\sqrt{14}\cos(x+\arctan(-\frac{3}{\sqrt{5}})-2\pi)$ .

Varför får jag en felaktig förskjutning? Var i mina beräkningar har jag gjort fel?

Ska det inte vara

b = 2pi PLUS arctan(-3/sqr5)

Jag får tänka litet till

Du har markerat en vinkel theta. Den är cirka –40°. Det betyder att vinkeln b är ca 320°, dvs 360° + (–40°)

Jaha, så eftersom min vinkel theta är negativ måste jag addera den med 2pi istället för att ta bort den från 2pi?

Perioden är 2pi. Så har du en vinkel theta ska du alltid addera med n 2pi.

Men man förvirras när theta är negativ, då tror man att man ska subtrahera. Och det ska man, för det blir minus när man adderar något negativt.

Även om man som jag är ganska van, blir man gärna osäker.

Men om min vinkel thetha hade varit t.ex. 16 positiva grader, då borde man väl dra bort det från 2pi? T.ex. här löste jag det genom att dra bort theta från pi istället (eller jag kallade vinkeln något annorlunda men du fattar):

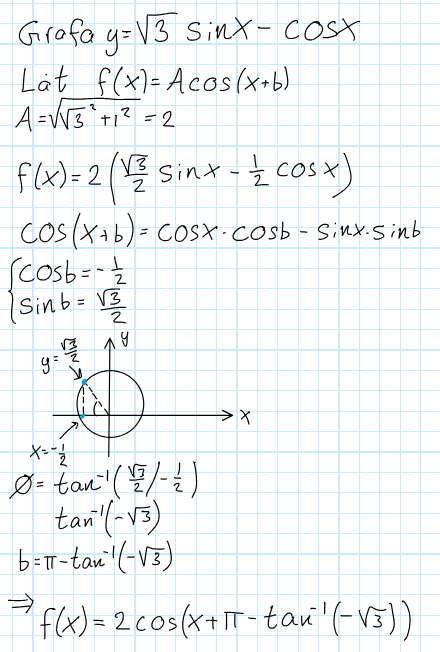
Tillägg: 28 sep 2023 07:54

Jag inser nu att det borde stå sinb = -sqrt3/2. Då kanske det blir som du säger.

Hej. Jag vet inte om detta redan är lvwrspelat och uppgiften är löst, men här kommer iallafall en beskrivning av hur jag skulle ha gjort.

Formeln $a\sin(x)+b\cos(x)=$

$=\sqrt{a^2+b^2}\sin(x+v)$ o.s.v. gäller då både $a$ och $b$ är positiva.

I vårt fall är $a=-3$ negativ,

Vi kan då skriva om uttrycket till det ekvivalenta $3\sin(-x)+\sqrt{5}\cos(-x)$ innan vi fortsätter.

Vifår då $\tan(v)=\frac{\sqrt{5}}{3}$ , dvs $v=\arctan(\frac{\sqrt{5}}{3})$

Uttrycket kan alltså skrivas $\sqrt{3^2+(\sqrt{5})^2}\sin(-x+\arctan(\frac{\sqrt{5}}{3}))$

Nu kan vi utnyttja att $\cos(v)=\sin(\frac{\pi}{2}-v)$ , vilket ger oss att uttrycket kan skrivas $\sqrt{14}\cos(x+\frac{\pi}{2}-\arctan(\frac{\sqrt{5}}{3}))$

Varför gäller det endast då a och b är negativa? Jag tänker att man kommer fram till uttrycket för A på följande sätt:

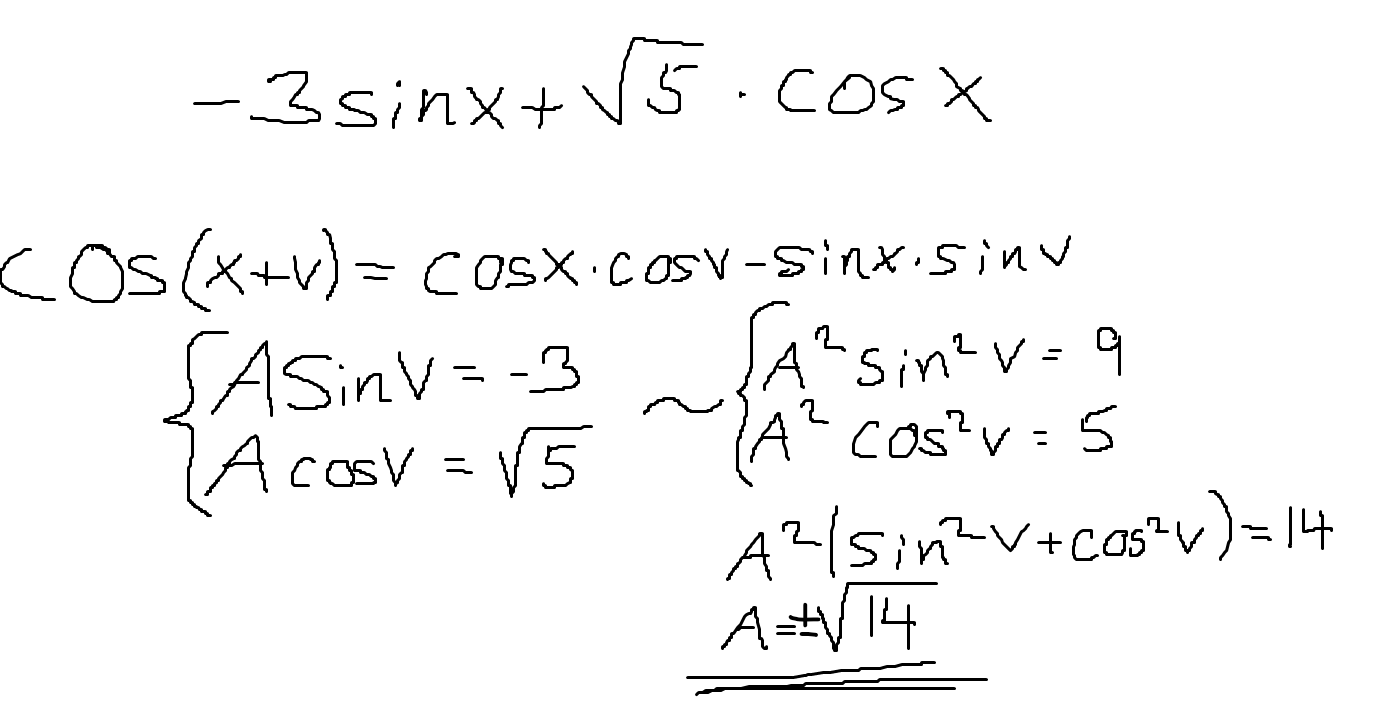
Då får man ju samma svar ändå trots att koefficienten är negativ. Man kvadrerar ju ändå det som står inuti så negativa tecken försvinner.

Skillnaden blir dels att argumentet x får annat tecken om en av a och b är negativ och att det spelar roll när du beräknar "hjälpvinkeln" v ur tan(v) = b/a.

Jaha, okej. Så för att en sådan här uppgift ska gå att lösa sådär smidigt måste man kunna skriva om funktionen så att $a$ och $b$ är positiva?

Och sedan måste väl även k vara samma i både cosinusfunktionen och sinusfunktionen?

Och vad betyder kravet här?:

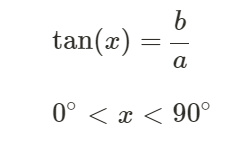
Betyder det att hjälpvinkeln kommer ligga i det intervallet? För det står att det gäller NÄR x ligger i det intervallet men det kan man väl omöjligen veta från början.

Eftersom både a och b är positiva så blir kvoten b/a ett positivt tal.

Att tan(x) är ett positivt tal innebär att x ligger antingen i första eller i tredje kvadranten.

Villkoret 0° < x < 90° begränsar nu x till första kvadranten.

Varför begränsar vi x till första kvadranten?

Tillägg: 28 sep 2023 11:54

T.ex. i det här klippet:

https://youtu.be/lt8R094MyPs?si=32XtwptDsjRVszPH

så bryr han sig inte om att koefficienterna inte är positiva. Varför blir det rätt ändå?

EDIT: jag fattar. Tack för hjälpen.

Tillägg: 28 sep 2023 17:25

Whoops jag skrev i redigera-läget men det blev en egen post…?

naytte skrev:
EDIT: jag fattar. Tack för hjälpen.

Vad bra.

Tillägg: 28 sep 2023 17:25

Whoops jag skrev i redigera-läget men det blev en egen post…?

Efter två timmar går det inte längre att redigera.

Svara

Visa senaste svar